Hans Walser, [20140312]

Verallgemeinerung der Parabel

Anregung: Wynands, 2014, S. 21, Aufgabe 2

1     Eine Folge von Šhnlichen rechtwinkligen Dreiecken

Im kartesischen Koordinatensystem zeichnen wir ein Dreieck mit en Ecken , , . Wir haben einen offenen Parameter t. In der Abbildung 1a ist  gewŠhlt worden.

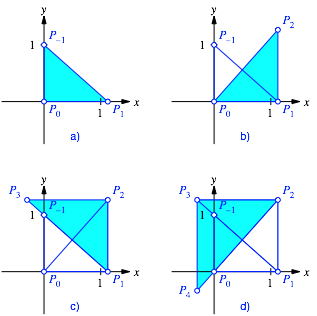
Abb. 1: €hnliche Dreiecke

Weiter zeichnen wir ein zum Dreieck  Šhnliches Dreieck  (Abb. 1b). Wir iterieren den Prozess: zum Dreieck  zeichnen wir ein Šhnliches Dreieck . Die Abbildung 1 zeigt die ersten Schritte.

2     Spiralen

Es entsteht eine eckige logarithmische Spirale (Abb. 2).

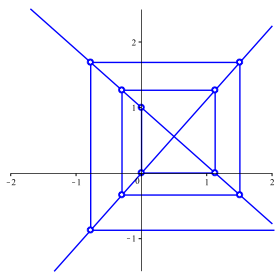
Abb. 2: Eckige Spirale

Die Punkte  liegen aber auch auf einer runden logarithmischen Spirale (Abb. 3).

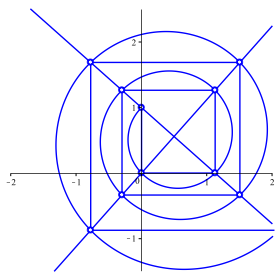
Abb. 3: Logarithmische Spirale

3     Parabel

Wir hatten fźr die ersten drei Punkt die Koordinaten festgelegt:

 

 

Dabei ist t ein noch freier Parameter. Wenn wir t variieren, bewegt sich der Punkt  auf der x-Achse.

Fźr den nŠchsten Punkt  ergeben sich auf Grund der €hnlichkeitskonstruktion die Koordinaten . Wenn wir also den Parameter t variieren, bewegt sich der Punkt  auf der quadratischen Parabel .

Die Abbildung 4 zeigt die Bahnkurven von  und .

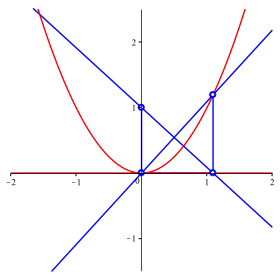
Abb. 4: Die Parabel erscheint

4     Weitere Kurven

Fźr die nachfolgenden Punkte erhalten wir die Koordinaten:

 

 

 

 

 

 

 

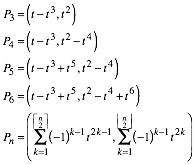
Die folgenden Abbildungen zeigen die zugehšrigen Kurven, die sich durch Variation von t ergeben.

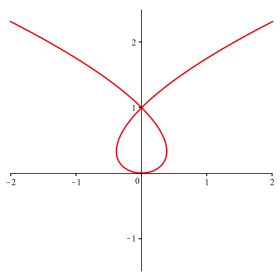
Abb. 5: n = 3

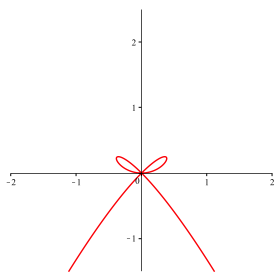
Abb. 6: n = 4

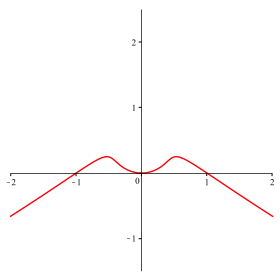
Abb. 7: n = 5

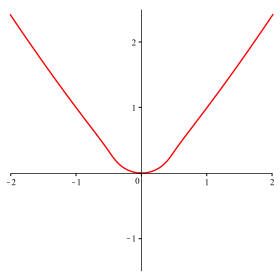
Abb. 8: n = 6

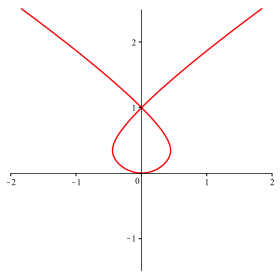
Abb. 9: n = 7

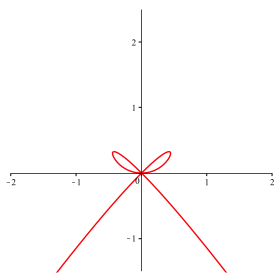
Abb. 10: n = 8

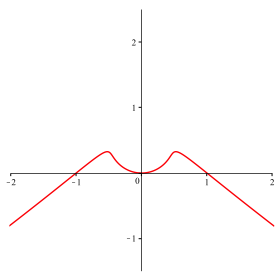
Abb. 11: n = 9

Die Abbildung 12 zeigt eine †berlagerung der FŠlle n = 0, ... , 9 fźr t aus dem Intervall [­–1, 1]. Wir sehen, dass sich ein gewisses Grundmuster modulo 4 wiederholt.  

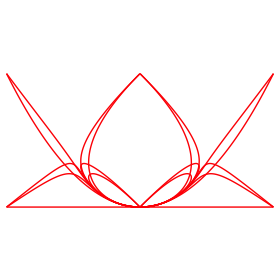
Abb. 12: n = 0, ... , 9

Im Folgenden noch einige grš§ere Werte fźr n.

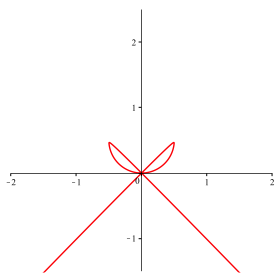
Abb. 13: n = 80

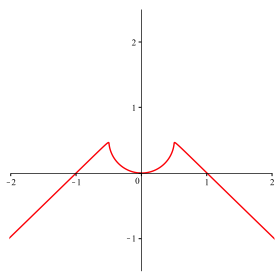
Abb. 14: n = 81

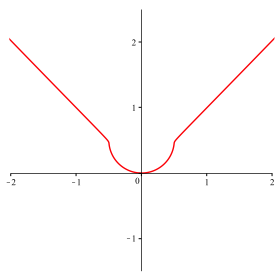
Abb. 15: n = 82

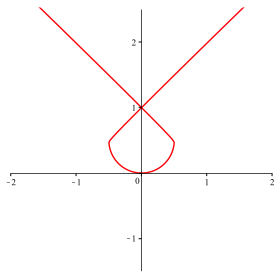
Abb. 16: n = 83

Die Abbildung 18 zeigt die †berlagerung der FŠlle n = 80, ... , 83.

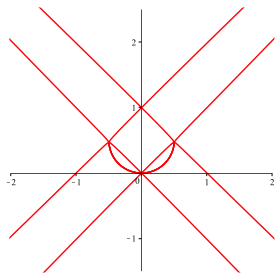
Abb. 17: n = 80, ... , 83

Wo ist der obere Halbkreis geblieben? Die Abbildung 18 zeigt die Situation fźr .

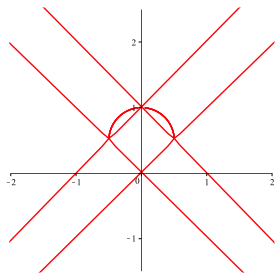
Abb. 18: n = –83, ... , –80

Literatur

Wynands, Alexander (2014): Mathematische (Basis-)Kompetenzen im Abitur.
(Un-)Verzichtbare Mathematik fźr ăAllgemeinbildungŇ und Hochschulzugang. GDM-Mitteilungen 96, 2014. S. 19-23.