Hans Walser, [20140726], [20140810], [20190514]

Verallgemeinerung des Satzes von Pythagoras

Hinweis: H. Sch., W.

1 Ecke abschneiden

Wir schneiden von einem Würfel eine Ecke ab (Abb. 1).

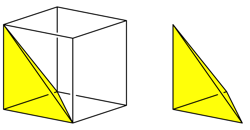
Abb. 1: Ecke abschneiden

Das abgeschnittene Stück ist ein unregelmäßiger Tetraeder. Drei Kanten sind so lang wie die Würfelkante und bilden eine ehemalige Würfelecke. Sie sind also paarweise senkrecht. Je zwei dieser drei Kanten spannen ein rechtwinklig gleichschenkliges Dreieck auf (blau in Abb. 2).

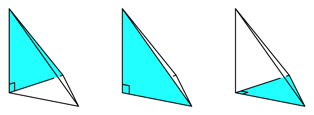
Abb. 2: Drei rechtwinklig gleichschenklige Dreiecke

Die drei restlichen Kanten des Tetraeders sind die Hypotenusen der drei rechtwinklig gleichschenkligen Dreiecke und haben somit eine Länge, die mal so groß ist wie die Würfelkante. Diese restlichen drei Kanten des Tetraeders spannen daher ein gleichseitiges Dreieck auf (rot in Abb. 3).

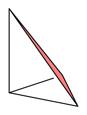
Abb.3: Gleichseitiges Dreieck

2 Flächeninhalte

Wie groß sind die Flächeninhalte all dieser Dreiecke?

Wir geben der Würfelkante die Länge 1. Für die drei blauen rechtwinklig gleichschenkligen Dreiecke erhalten wir damit je eine halbe Quadratfläche, also je . Der Flächeninhalt eines gleichseitigen Dreieckes mit der Seitenlänge kann mit der Formel

berechnet werden. In unserem Beispiel (rotes Dreieck) ist und wir erhalten:

Stellen wir dies in einer Tabelle ordentlich dar (Tab. 1). In der letzten Spalte sind auch noch die Quadrate der Flächeninhalte eingetragen.

Dreiecktyp	Flächeninhalt	Quadrat davon
Rechtwinklig gleichschenklig
Rechtwinklig gleichschenklig
Rechtwinklig gleichschenklig
Gleichseitig

Tab. 1: Übersicht

Wir sehen, dass die Summe der Quadrate der drei blauen Flächeninhalte gleich dem Quadrat des roten Flächeninhaltes ist.

3 Quadrate von Flächeninhalten

Wenn wir mit Maßeinheiten arbeiten, also etwa mit einem Würfel der Kantenlänge 1cm, erhalten wir für den Flächeninhalt der drei blauen rechtwinklig gleichschenkligen Dreiecke erhalten wir je . Das „Quadrat“ davon ist . Das Wort „Quadrat“ ist also nicht im geometrischen Sinne eines Vierecks mit vier gleich langen Seiten und vier rechten Winkeln zu verstehen, sondern algebraisch als Multiplikation einer Größe mit sich selber. Das Quadrat eines Flächeninhaltes spielt daher im vierdimensionalen Raum und kann nicht mehr geometrisch gezeichnet werden. Wir haben es mit einer Abstraktion zu tun.

4 Nochmals Ecke abschneiden

Wir schneiden nun die Würfelecke weniger regelmäßig ab (Abb. 4). Es entsteht ein unregelmäßiges Tetraeder . Die drei Kanten , und sind nun nicht mehr gleich lang, stehen aber immer noch paarweise senkrecht aufeinander. Der Punkt C liegt in der rechten Raumecke.

Wir erhalten so ein Analogen zu einem ebenen rechtwinkligen Dreieck.

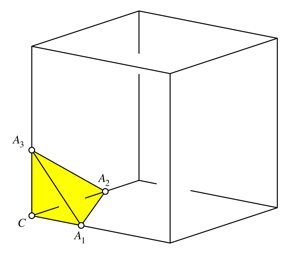
Abb. 4: Analogon zum rechtwinkligen Dreieck

Drei der vier Seitenflächen des Tetraeders sind rechtwinklige Dreiecke. Diese drei Seitenflächen übernehmen die Rollen der Katheten (Abb. 5). Sie liegen den drei Ecken , und gegenüber.

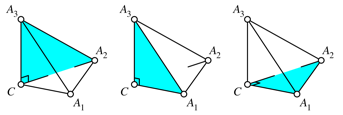
Abb. 5: Kathetenflächen

Die vierte Seitenfläche, ein spitzwinkliges Dreieck, übernimmt die Rolle der Hypotenuse (Abb. 6). Sie liegt der Ecke C gegenüber.

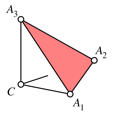
Abb. 6: Hypotenusenfläche

5 Analogon zum Satz des Pythagoras

Es gilt das Theorem:

In einem Tetraeder mit drei rechten Winkeln an einer Ecke ist die Summe der Quadrate der Kathetenflächeninhalte gleich dem Quadrat des Hypotenusenflächeninhaltes.

Durch das Quadrieren der Flächeninhalte entstehen Gebilde im vierdimensionalen Raum. Wir können also nicht wie beim Satz des Pythagoras in der Ebene das Theorem mit angesetzten geometrischen Quadraten illustrieren.

6 Beweis des Theorems

Wir verwenden die Bezeichnungen der Abbildung 7 und passen die Figur in ein kartesisches Koordinatensystem mit dem Ursprung in C ein.

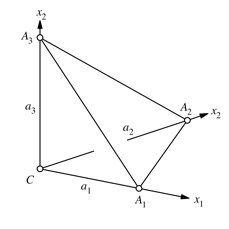
Abb. 7: Bezeichnungen. Kartesisches Koordinatensystem

Für die Kathetenflächen erhalten wir der Reihe nach:

Somit ist:

Für die Berechnung der Hypotenusenfläche verfahren wir wie folgt: Die Ebene durch die drei Punkte , und hat die Gleichung:

Diese Gleichung formen wir zur Hesseschen Normalform um:

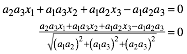
Damit hat C den Abstand

von der Ebene. Das ist aber auch die Höhe des Tetraeders bezogen auf die Hypotenusenfläche H.

Der Tetraeder hat das Volumen:

Andererseits ist:

Vergleich ergibt für die Hypotenusenfläche H:

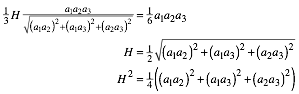
Somit ist:

7 Frage der Umkehrung

In der ebenen Geometrie gilt der Satz des Pythagoras in beiden Richtungen:

Unser räumliches Analogon gilt leider nur in einer Richtung:

Im Folgenden ein Gegenbeispiel für die Ungültigkeit der Umkehrung.

Es sei zunächst , , und . Dies ist das Einführungsbeispiel der Abbildungen 1 bis 3.

Es ist und . Wir haben bei C drei rechte Winkel und es ist .

Die Punkte, von denen aus die Strecken , und je unter einem rechten Winkel gesehen werden, liegen auf den drei Thaleskugeln über diesen Strecken. Diese drei Kugeln haben genau zwei Punkte gemeinsam, nämlich und . Der zweite Punkte ist der Spiegelpunkt von C bei Spiegelung an der Ebene durch die drei Punkte , und .

Und nun das Gegenbeispiel: Die drei Punkte , und und damit den Flächeninhalt H lassen wir unverändert. Den Punkt C variieren wir zu , berechnen die drei Flächeninhalte der Dreiecke mit einer Ecke in C und zwei weiteren Ecken in den Punkten , und (diese Dreiecke sind in der Regel nicht rechtwinklig) und verlangen schließlich, dass die Summe der Quadrate dieser Flächeninhalte dem Quadrat von H entspricht. Dies führt mit einiger Rechnung auf die Bedingung:

Diese Bedingung beschreibt eine sogenannte Quadrik und zwar ein abgeplattetes Rotationsellipsoid (also wie die Erde) mit den Punkten und in den beiden Polen (Abb. 7). Alle Punkte auf diesem Ellipsoid erfüllen die Flächenbedingung, aber nur die beiden Pole führen auf drei rechte Winkel.

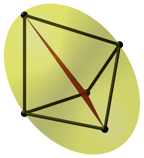
Abb. 8: Ellipsoid

Die drei Punkte , und liegen ebenfalls auf dem Ellipsoid.

Die Abbildung 9 zeigt verschiedene spezielle Sichten des Ellipsoides. Es ist zusätzlich der Äquator des Ellipsoides eingezeichnet.

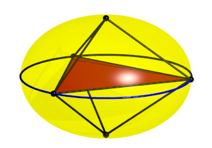
Abb. 9.1: Senkrecht stehende Achse

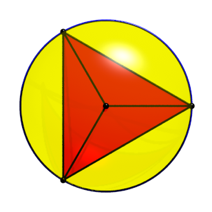
Abb. 9.2: Sicht in Richtung der Achse

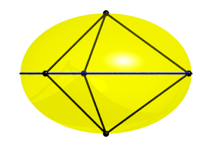
Abb. 9.3: Allgemeine Sicht von der Seite

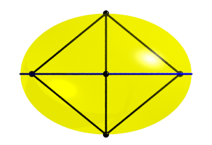
Abb. 9.4: Spezielle Sicht von der Seite

Im Achsenschnitt (Abb. 9.3 und 9.4) sehen wir die Abplattung. Die lange Ellipsenachse verhält sich zur kurzen Ellipsenachse wie . Die Ellipse lässt sich also in ein Rechteck im DIN-Format einpassen (Walser 2013).

8 Im vierdimensionalen Raum

Das Theorem lässt sich in höhere Dimensionen verallgemeinern.

Wir arbeiten im mit der konvexen Hülle der fünf Punkte . , , und . Dies ist ein 4-Simplex.

Die vier Kathetentetraeder entstehen als konvexe Hülle von C und drei der vier Punkte . Sie haben der Reihe nach die Volumina:

Das Hypotenusentetraeder ist die konvexe Hülle der vier Punkte .

Die Hyperebene durch die vier Punkte hat die Gleichung:

Für den Abstand des Ursprungs C von dieser Hyperebene erhalten wir:

Nun gilt für das 4d-Volumen des 4-Simplexes einerseits:

Andererseits ist:

Vergleich ergibt:

Daraus folgt:

9 Allgemein

Für den n-dimensionalen Fall ist das jetzt nur noch eine langweilige Schreibübung.

Wir arbeiten im mit der konvexen Hülle der Punkte , , , ... , . Dies ist ein n-Simplex.

Die n Katheten-(n–1)-Simplexe sind die konvexen Hüllen von C und der n Punkte . Sie haben die (n–1)-d-Volumina :

Das Hypotenusen-(n–1)-Simplex ist die konvexe Hülle der n Punkte .

Die Hyperebene durch die n Punkte hat vom Ursprung C den Abstand:

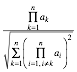
Für das n-d-Volumen des n-Simplexes erhalten wir einerseits:

Andererseits ist:

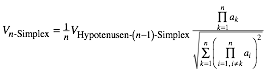
Vergleich ergibt:

Daraus folgt:

10 Regelmäßige Simplexe

Wenn wir im sämtliche wählen, erhalten wir ein regelmäßiges Hypotenusen-n-Simplex der Kantenlänge 1.

Sein n-d-Volumen H kann nun mit dem verallgemeinerten Theorem des Pythagoras berechnet werden.

Zunächst ist . Somit ist:

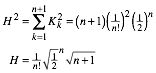
Die Tabelle 2 zeigt einige Resultate.

n	H
1	1	Strecke
2		Gleichseitiges Dreieck
3		Regelmäßiges Tetraeder
4
5
6
7		rational
8		rational
9
10

Tab. 2: Volumina regelmäßiger n-Simplexe

Die n-d-Volumina der n-Simplexe tendieren gegen null.

Literatur

Walser, Hans (2013): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Edition am Gutenbergplatz, Leipzig 2013. ISBN 978-3-937219-69-1.