Hans Walser, [20091121a]
Verdrehtes Kreissegment
1 Worum es geht
Wir drehen ein
Kreissegment um eine Ecke um einen beliebigen Winkel.
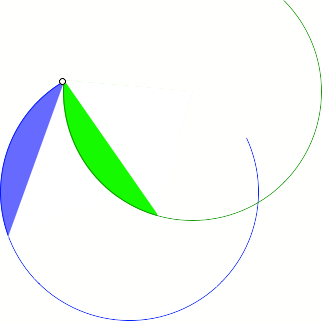
Verdrehtes Kreissegment
Dann sind die andere
Segmentecke, ihr verdrehtes Bild und der Schnittpunkt der beiden TrŠgerkreise
der Segmente kollinear.
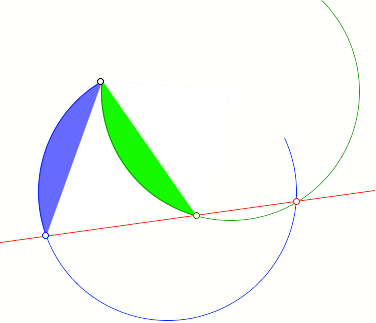
Kollineare Punkte
2
Beweis
Bezeichnungen gemŠ§
Figur. Der Drehpunkt ist A; 
sei der
verdrehte Punkt 
.
Die TrŠgerkreise 
und 
haben die beiden
Schnittpunkte A (Drehpunkte) und S.
Wir zeigen, dass der
Schnittpunkt 
von BS mit 
mit dem Punkt 
zusammenfŠllt.
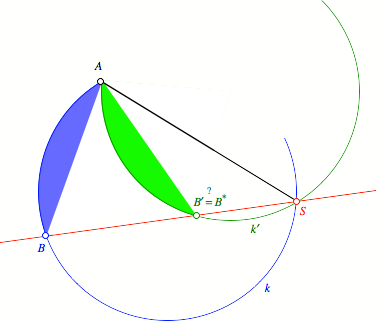
Beweisfigur
Der Kreisbogen 
von 
und der
Kreisbogen 
von 
sind
ErgŠnzungsbogen mit dem gleichen Radius. Wir interpretieren diese als Ortsbogen
(Fasskreise) źber der Strecke AS. Die zugehšrigen
Peripheriewinkel sind dann ErgŠnzungswinkel auf ą. Es ist also:
Daher ist:
Das Dreieck 
ist also
gleichschenklig, die Strecken 
und 
gleich lang.
Andererseits sind auch die Sehnen 
und 
gleich lang.
Daher ist 
.
3
Verdrehtes Kreisbźschel
Wir verdrehen ein
Kreisbźschel gemŠ§ Figur.
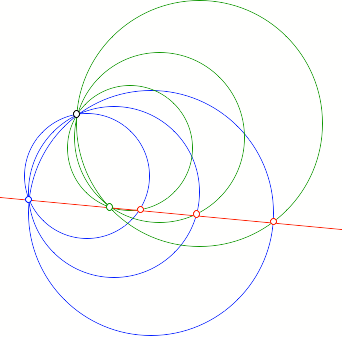
Verdrehtes Kreisbźschel
Die Schnittpunkte
entsprechender Kreise sind kollinear.
4
Verdrehte Sehnenvielecke
Wenn wir eine
Sehnenvieleck um eine Punkt des Umkreises drehen, sind die Verbindungsgeraden
entsprechender Eckpunkte kopunktal.
4.1
Sehnenviereck
Als Beispiel ein Sehnenviereck.
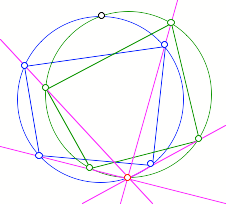
Verdrehtes Sehnenviereck
4.2
RegelmŠ§iges Vieleck
Als Sonderfall kšnnen
wir ein regelmŠ§iges Vieleck um eine Ecke drehen.
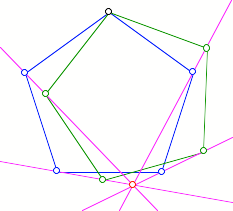
Verdrehtes Fźnfeck