Hans Walser, [20181021]
Verdrehtes Kreuzgewlbe
1 Worum geht es?
Analogien zu [2] und [3]. Verallgemeinerung von [1].
2 Schnitt zweier Zylinder
Die Abbildung 1a zeigt die Durchschnittsfigur zweier Zylinder. Die beiden Zylinder haben je den Radius 1. Ihre Achsen schneiden sich orthogonal.
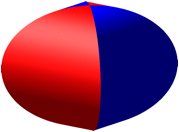
a) b)
Abb. 1: Durchschnitt zweier Zylinder. Kreuzgewlbe
Gem§ [1]
hat die Figur das Volumen ![]() und die
Oberflche 16. Bei beiden Resultaten kommt die Kreiszahl ¹ nicht vor.
und die
Oberflche 16. Bei beiden Resultaten kommt die Kreiszahl ¹ nicht vor.
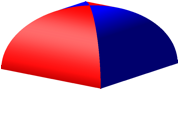
Die obere Hlfte der Figur kann als Kreuzgewlbe interpretiert werden (Abb. 1b).
Die horizontalen Querschnitte sind Quadrate (Abb. 2). Diese Quadrate sind zur Volumenberechnung hilfreich. Wir knnen das Prinzip von Cavalieri anwenden.
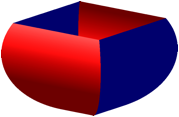
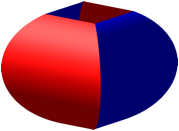
Abb. 2: Querschnitte je ein Quadrat
3 Verdrehung
Die Abbildung 3 zeigt nun eine Verdrehung der Figur.
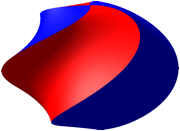
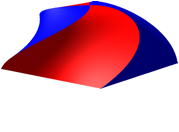
Abb.3: Verdrehte Figur
Die Querschnitte sind immer noch Quadrate, aber gegeneinander verdreht (Abb. 4).

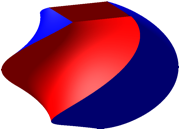
Abb. 4: Querschnitte sind Quadrate
Das hei§t, dass sich das Volumen beim Verdrehen nicht ndert. Hingegen wird die Oberflche gr§er.
4 Inkugel und vivianische Kurve
Die Figur der Abbildung 1a hat die Einheitskugel als Inkugel. Die Berhrung erfolgt an ausgewhlten Meridianen der Inkugel (Abb. 5).
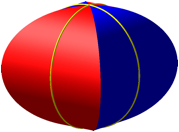
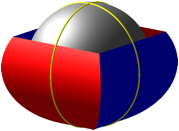
Abb. 5: Berhrmeridiane und Inkugel
Durch die Verdrehung werden die Berhrkurven zu so genannten vivianischen Kurven verdreht (Abb. 6).
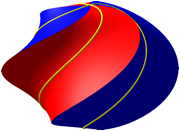
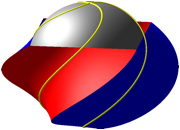
Abb. 6: Vivianische Kurven
5 Strkere Verdrehung
Die Abbildung 7 zeigt eine Verdrehung, die das Vierfache der Verdrehungen der Abbildungen 3 und 6 ausmacht.

Abb. 7: Starke Verdrehung
6 Oberflchenberechnungen
Die unverdrehte Figur hat die Oberflche 16. Bei Verdrehen wird die Oberflche gr§er.
Wir fhren einen Verdrehungsparameter k ein. Fr k = 0 haben wir keine Verdrehung (Abb. 8a). Fr k = 1 haben wir zwischen den Polen eine Verdrehung um 180¡ (Abb. 8b). Allgemein haben wir zwischen den Polen eine Verdrehung um k mal 180¡.

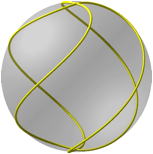
a) b)
Abb. 8: Verdrehungen illustriert durch vivianische Kurven
In den Abbildungen 3 und 6 ist k = 1, in der Abbildung 7 haben wir k = 4. In Abhngigkeit von k haben wir fr eine der beiden roten Flchenstcken die Parameterdarstellung:
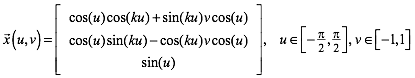 (1)
(1)
Daraus ergeben sich die partiellen Ableitungen:
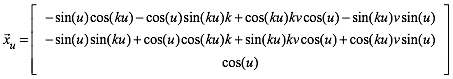 (2)
(2)
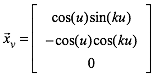 (3)
(3)
Daraus ergibt sich fr die erste Fundamentalform:
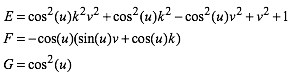 (4)
(4)
Weiter ist:
![]() (5)
(5)
Das rote Flchenstck hat somit den Flcheninhalt:
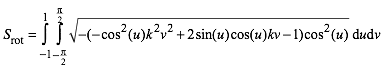 (6)
(6)
Die gesamte Oberflche ist das Vierfache davon.
Die Tabelle 1 gibt die ersten numerischen Werte.
|
k |
Oberflche |
|
0 |
16.00000000 |
|
1 |
17.34942539 |
|
2 |
20.78373017 |
|
3 |
25.36702411 |
|
4 |
30.54973100 |
|
5 |
36.06661631 |
|
6 |
41.78547584 |
|
7 |
47.63508760 |
|
8 |
53.57411592 |
Tab. 1: Numerische Werte
Links
[1] Hans Walser: Rund ohne ¹
http://www.walser-h-m.ch/hans/Miniaturen/R/Rund_ohne_Pi/Rund_ohne_Pi.htm
[2] Hans Walser: Verdrehter Wrfel
www.walser-h-m.ch/hans/Miniaturen/V/Verdrehter_Wuerfel/Verdrehter_Wuerfel.htm
[3] Hans Walser: Verdrehtes Tetraeder
www.walser-h-m.ch/hans/Miniaturen/V/Verdrehtes_Tetraeder/Verdrehtes_Tetraeder.htm