Hans Walser, [20170124]
Vergrš§ern mit dem Goldenen Schnitt
Anregung: Heinz Klaus Strick, Leverkusen
1 Worum geht es?
Wir
beginnen mit einem regelmŠ§igen n-Eck
und verlŠngern die Seiten zyklisch in einer Richtung mit dem Faktor 
(Goldener
Schnitt). Die Au§enecken verbinden wir zu einem grš§eren n-Eck. Die Abbildung 1 zeigt das Vorgehen fŸr n = 3, 4, 5, 6. Vgl. (Walser 2013, S. 56).
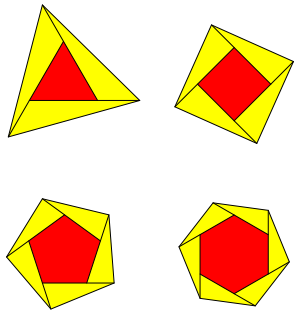
Abb. 1: Vergrš§ern der Vielecke
2 FlŠchenzuwachs
Wir fragen, wie sich der gelbe Zuwachs im Vergleich zur roten AusgangsflŠche verhŠlt. Im regelmŠ§igen n-Eck finden wir mit etwas Rechnung fŸr dieses VerhŠltnis fn:
(1)
Die Tabelle 1 zeigt die ersten Werte.
|
n |
fn |
Bemerkungen |
|
3 |
3 |
exakt |
|
4 |
2 |
exakt |
|
5 |
1.381966012 |
|
|
6 |
1 |
exakt |
|
7 |
0.7530203968 |
|
|
8 |
0.5857864380 |
|
|
9 |
0.4679111136 |
|
|
10 |
0.3819660113 |
|
|
11 |
0.3174929345 |
|
|
12 |
0.2679491924 |
|
Tab. 1: Werte
Die FŠlle fŸr n = 3 und n = 4 dŸrften bekannt sein. Der schšne Fall n = 6 war mir bis anhin nicht bekannt. Wir kšnnen also mit dem Goldenen Schnitt die SechseckflŠche verdoppeln.
3 Detail
UnabhŠngig von n gilt: Ein einzelner Zuwachsspickel ist flŠchengleich zum Dreieck welches im n-Eck von der kŸrzesten Diagonale abgeschnitten wird (Abb. 2).
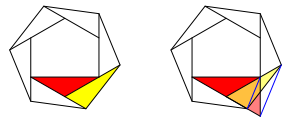
Abb. 2: FlŠchengleichheit
Der Beweis ergibt sich aus
(2)
Damit kšnnen die ãschšnenÒ FŠlle n = 3, 4, 6 ohne Rechnung nachgewiesen werden.
4 Quadratwurzel aus 2
FŸr n = 6 hat das gro§e Sechseck den
doppelten FlŠcheninhalt wie das kleine. Damit ist die gro§e SeitenlŠnge das 
der
kleinen SeitenlŠnge.
Somit
haben wir einen Link zwischen dem Goldenen Schnitt und der Zahl 
. Vgl. dazu (Walser 2013, S. 13, Abb. 1.1c)
Literatur
Walser, Hans (6. Auflage). (2013). Der Goldene Schnitt. Mit einem Beitrag von Hans Wu§ing Ÿber populŠrwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.