Hans Walser, [20210316]
Verschnrung
Anregung: Jentsch et alii 2021
1 Worum geht es?
Stabile, indifferente und labile Verschnrungen
2 Das Beispiel
In Jentsch et alii (2021), S. 117, sticht eine Figur fast sprichwrtlich ins Auge. Es geht um Folgendes: ãZwei Geschenkschachteln sind mit Bndern verschnrt, wie unten dargestellt. Schachtel A ist ein Wrfel mit der Seitenlnge 10 cm. Schachtel B ist ein Zylinder, dessen Hhe und Durchmesser ebenfalls 10 cm betragen.
Fr welche der beiden Schachteln wird mehr Band bentigt?
Erklren Sie, wie Sie zu der Antwort gekommen sind.Ò
Die Abbildung 1 zeigt eine Nachzeichnung des Autors, wobei die offensichtlichen Ungereimtheiten der Originalzeichnung stillschweigend korrigiert wurden.
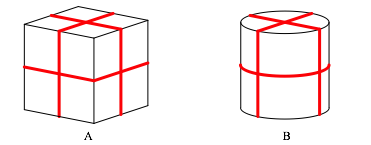
Abb. 1: Verschnrungen
Zur pdagogischen Befriedigung der Lehrperson muss man natrlich sagen, dass A (der Wrfel also) mehr Band braucht, wie man durch Ineinanderstellen der beiden Schachteln sofort sieht (Abb. 2). Der Wrfel braucht einen lngeren Bauchgurt.
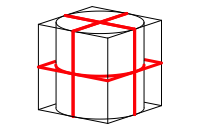
Abb. 2: Der Wrfel braucht mehr Band
So weit so gut.
3 Wer keine Vergangenheit hat, hat keine Zukunft
Jede und jeder von uns hat seit ihrer oder seiner Jugend schon einige verschnrte wrfelfrmige und allgemein viele verschnrte quaderfrmige Geschenkschachteln erhalten oder verschenkt.
Ich gestehe aber, dass ich in meinem Leben noch keine einzige verschnrte zylinderfrmige Schachtel gesehen habe. Um dies in etwa nachzuholen, habe ich versucht eine zylinderfrmige Farbdose zu verschnren. Wenn Sie, liebe Leserin, lieber Leser, dies noch nie versucht haben, geht Ihnen die Betroffenheitskompetenz ab, den Rest dieser Glosse zu lesen.
Die Schnur rutschte immer wieder ab. Am Schluss ging es dann noch, aber nur, weil die schon recht rostige Farbdose einen hohen Haftreibungskoeffizienten gegenber der Schnur hatte.
Bei der Verschnrung des Zylinders haben wir es mit einer am Schreibtisch ausgedachten ãLehreraufgabeÒ zu tun. Sie ist in der Schule durchaus lsbar, im Alltag kaum.
Anders ist die Situation bei der Verwendung von Klebestreifen anstelle der Bnder.
4 Indifferente und labile Verschnrungen
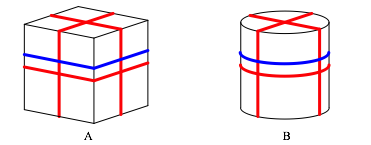
Abb. 3: Verschieben des Bauchgurtes
Wenn wir den Bauchgurt der beiden Verschnrungen etwas nach oben oder nach unten verschieben, ndert sich seine Lnge nicht (Abb. 3).
Anders sieht die Sache aus beim Verschieben einer der beiden anderen Schlingen um die Schachteln (Abb. 4).
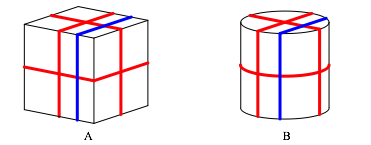
Abb. 4: Verschieben einer anderen Schlinge
Beim Wrfel ndert sich nach wie vor nichts.
Beim Zylinder aber kann die verschobene Schlinge verkrzt werden oder anders gesagt, die bisherige Schlinge ist zu lang, wird locker und rutscht ab.
Beim Wrfel haben wir somit eine Verschnrung, die gegen kleine Verschiebungen indifferent ist.
Beim Zylinder hingegen haben wir eine labile Verschnrung. Bei der kleinsten Verschiebung rutscht sie ab.
Nun ja, eine stabile Verschnrung ergibt sich etwa bei der sprichwrtlichen Schlinge um den Hals. Eine todsichere Sache.
Die Abbildung 5a zeigt eine labile Verschnrung des Wrfels.

Abb. 5: Labile Wrfelverschnrung. Lockere Schlingen
In der Abbildung 5b sind einige Schlingen nicht angespannt und zu lang. Sei werden sofort locker.
5 Vernetzung
Wir knnen die einzelnen Schlingen an den Kreuzungsstellen verknoten (Abb. 6).
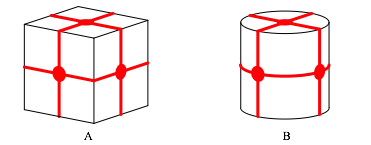
Abb. 6: Netz
Dadurch entsteht ein der Schachtel angepasstes Netz, bei dem das Abrutschen durch die Knoten verhindert wird. Das ist ein anderes Paar Stiefel.
Literatur
Jentsch, Armin & Schlesinger, Lena & Heinrichs, Hannah & Kaiser, Gabriele & Knig, Johannes & Blmeke, Sigrid (2021): Erfassung der fachspezifischen Qualitt von Mathematikunterricht: Faktorenstruktur und Zusammenhnge zur professionellen Kompetenz von Mathematiklehrpersonen. Journal fr Mathematik-Didaktik, 42, 79-121.