Hans Walser, [20210720]
Vielecke einpacken
0 Worum geht es?
Regelmäßige Vielecke sollen von regelmäßigen Vielecken eingepackt werden.
1 Beispiele
Ein gleichseitiges Dreieck kann von drei regelmäßigen Zwölfecken eingepackt werden, ein Quadrat von vier regelmäßigen Achtecken (Abb. 1).
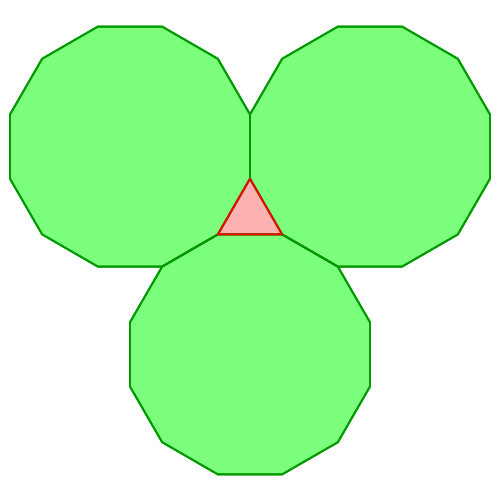
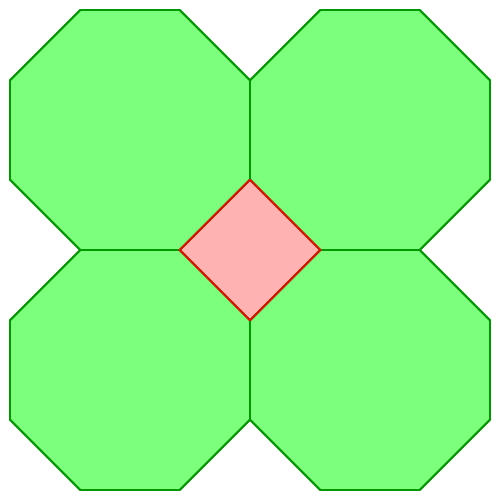
Abb. 1: Eingepacktes Dreieck und eingepacktes Viereck
Gibt es weitere Beispiele?
Experimentell finden wir noch zwei weitere Beispiele (Abb. 2).
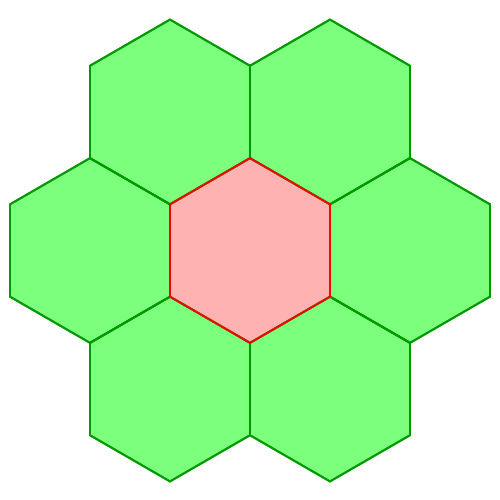
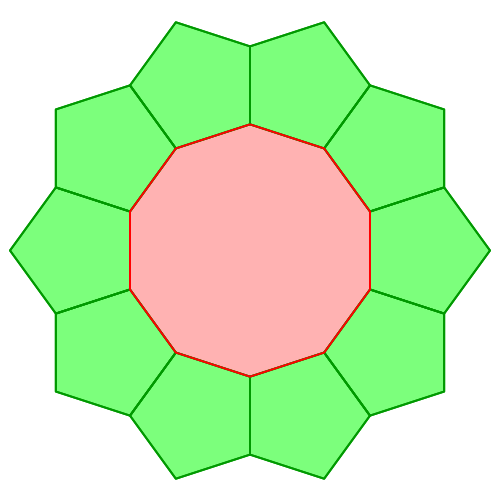
Abb. 2: Sechseck und Zehneck
Weitere Beispiele scheint es nicht zu geben.
2 Bearbeitung
Wir wollen ein regelmäßiges n-Eck einpacken. Es hat den Außenwinkel a :
![]() (1)
(1)
Somit erhalten wir für den Innenwinkel b eines Verpackungsvieleckes:
![]() (2)
(2)
Der
Außenwinkel g des Verpackungsvieleckes und damit sein Zentriwinkel ist:
![]() (3)
(3)
Daraus ergibt sich für die
Eckenzahl en des Verpackungsvieleckes:
![]() (4)
(4)
Die Tabelle 1 gibt die ersten
Werte für en.
|
n |
en |
en |
|
n |
en |
en |
|
3 |
12 |
12 |
|
22 |
22/5 |
4.4 |
|
4 |
8 |
8 |
|
23 |
92/21 |
4.380952381 |
|
5 |
20/3 |
6.666666667 |
|
24 |
48/11 |
4.363636364 |
|
6 |
6 |
6 |
|
25 |
100/23 |
4.347826087 |
|
7 |
28/5 |
5.6 |
|
26 |
13/3 |
4.333333333 |
|
8 |
16/3 |
5.333333333 |
|
27 |
108/25 |
4.32 |
|
9 |
36/7 |
5.142857143 |
|
28 |
56/13 |
4.307692308 |
|
10 |
5 |
5 |
|
29 |
116/27 |
4.296296296 |
|
11 |
44/9 |
4.888888889 |
|
30 |
30/7 |
4.285714286 |
|
12 |
24/5 |
4.8 |
|
31 |
124/29 |
4.275862069 |
|
13 |
52/11 |
4.727272727 |
|
32 |
64/15 |
4.266666667 |
|
14 |
14/3 |
4.666666667 |
|
33 |
132/31 |
4.258064516 |
|
15 |
60/13 |
4.615384615 |
|
34 |
17/4 |
4.25 |
|
16 |
32/7 |
4.571428571 |
|
35 |
140/33 |
4.242424242 |
|
17 |
68/15 |
4.533333333 |
|
36 |
72/17 |
4.235294118 |
|
18 |
9/2 |
4.5 |
|
37 |
148/35 |
4.228571429 |
|
19 |
76/17 |
4.470588235 |
|
38 |
38/9 |
4.222222222 |
|
20 |
40/9 |
4.444444444 |
|
39 |
156/37 |
4.216216216 |
|
21 |
84/19 |
4.421052632 |
|
40 |
80/19 |
4.210526316 |
Tab. 1: Eckenzahlen der Verpackungsvielecke
Für n = 3, 4, 6 und 10 ergeben sich die schon bekannten
Eckenzahlen der Abbildungen 1 und 2.
Die Folge en ist monoton abnehmend mit dem Grenzwert 4.
Daher gibt es keine weiteren ganzzahligen Lösungen für das Verpackungsvieleck
mehr. Zwischen e10 = 5 und dem Grenzwert 4 gibt es keine weiteren ganzen Zahlen. Basta
3
Sterne
In der zweiten Spalte der Tabelle 1 ist en als
gekürzter Bruch angegeben. Zum Beispiel ist e5 = 20/3. Wir können diesen Bruch als Stern
interpretieren. Auf einem Kreis werden 20 Punkte regelmäßig verteilt. Wir
starten in einem Punkt und gehen weiter zum dritten Punkt. Und so weiter
jeweils zum drittnächsten Punkt. So entsteht ein Stern (Abb. 3).
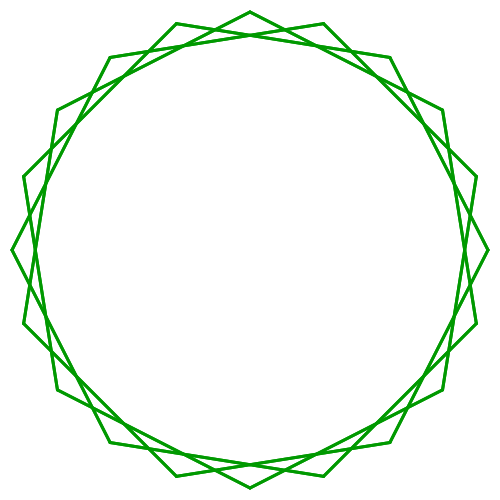
Abb. 3: Der 20/3-Stern
Wenn wir solche Sterne als Verpackungsvielecke zulassen, ergibt sich
auch für n = 5 eine Lösung (Abb. 4).
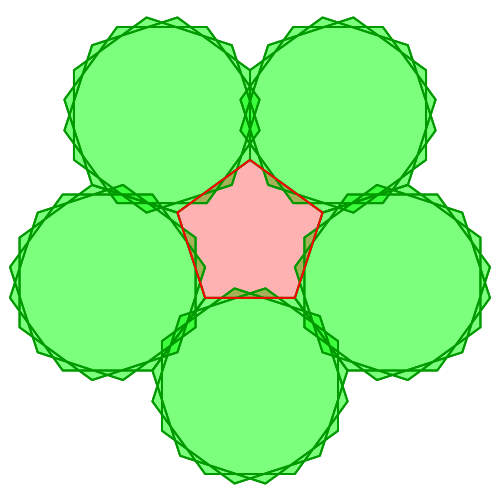
Abb. 4: Verpacktes Fünfeck
Analog können wir nun jedes regelmäßige Vieleck verpacken. Die Abbildung
5 zeigt das Beispiel des 18-Ecks mit 9/2-Sternen als Verpackungsmaterial.
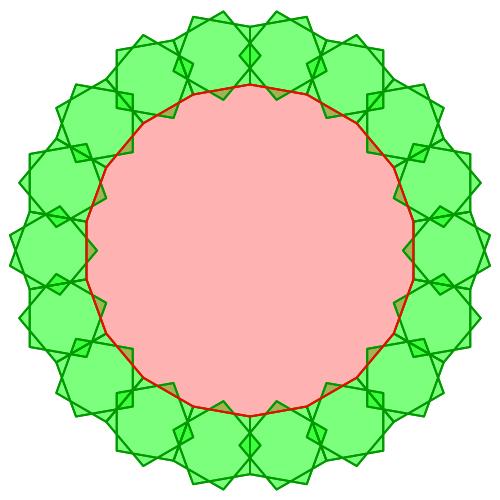
Abb. 5: 18-Eck und 9/2-Sterne