Hans Walser, [20091117a]
RegelmŠ§ige Vielecke mit Kreisen
1
Worum es geht
Einem regelmŠ§igen
Vieleck beliebiger Eckenzahl n wird ein
regelmŠ§iges Vieleck gleicher Eckenzahl eingeschrieben. Die Figur zeigt die
Situation fŸr FŸnfecke.
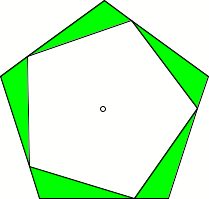
Situation
Unter den Ecken
entstehen n kongruente Dreiecke.
Wir interessieren uns
nun um die Inkreise und die Umkreise dieser Dreiecke.
2
Inkreise
Wir zeichnen die
Inkreise der kleinen Dreiecke.
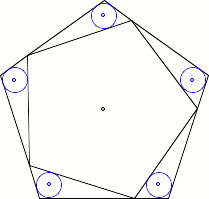
Inkreise
Die Zentren dieser
Inkreise liegen auf dem Umkreis des einbeschriebenen n-Eckes.
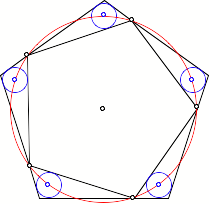
Zentren auf dem Umkreis
Dies gilt unabhŠngig
von der Eckenzahl n.
3
Umkreise
Und nun die Umkreise
der kleinen Dreiecke.
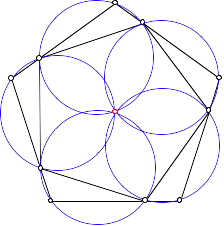
Umkreise
Die Umkreise verlaufen
durch den Mittelpunkt der Figur. Auch diese Eigenschaft ist unabhŠngig von n.
4
Beweise
Wir bezeichnen mit 
(zyklische
Nummerierung modulo n) die Ecken des
Šu§eren regelmŠ§igen n-Eckes. Ferner
seien 
mit 
die Ecken des
einbeschriebenen regelmŠ§igen n-Eckes,
die Inkreismittelpunkte
der Dreiecke 
und M der Mittelpunkt der Gesamtfigur. Die Figur zeigt
einen beweisrelevanten Ausschnitt.
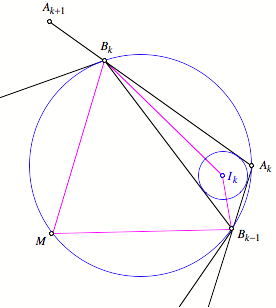
Beweisfigur
Das Dreieck 
hat
bei 
denselben
Au§enwinkel wie das regelmŠ§ige n-Eck,
also 
. Daher ist die Summe der beiden Dreieckswinkel bei 
und 
ebenfalls so
gro§:
Da der Inkreismittelpunkt
auf der
Schnittpunkt der Winkelhalbierenden der beiden Winkel 
und 
ist, erhalten
wir fŸr den Au§enwinkel des Dreieckes 
bei 
:
Der Punkt 
liegt also auf
dem Ortsbogen (Fasskreis) Ÿber der Strecke 
fŸr den
Au§enwinkel 
; dies ist aber wegen 
der Umkreis des
regelmŠ§igen n-Eckes 
. Damit ist die Aussage Ÿber die Inkreismittelpunkte der
Dreiecke 
bewiesen.
Im Viereck 
sind der
Innenwinkel bei M und der Au§enwinkel
bei 
gleich gro§,
nŠmlich 
. Das Viereck ist daher ein Sehnenviereck; der Kreis durch
die drei Punkte 
verlŠuft auch
durch M. Damit ist die Aussage
Ÿber die Umkreise der Dreiecke 
bewiesen.
5
Bildergalerie
Beispiele fŸr die
Eckenzahlen 3, 4, 6, 7.
5.1
RegelmŠ§iges Dreieck
Beim regelmŠ§igen
Dreieck liegen zusŠtzlich auch die Mittelpunkte der Umkreise der Dreiecke 
auf dem Umkreis
des einbeschriebenen regelmŠ§igen Dreiecks 
. Warum ist das so?
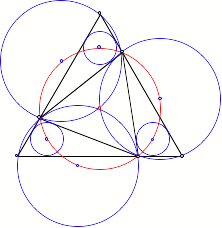
RegelmŠ§iges Dreieck
5.2
Quadrat
Beim Quadrat sind die
Mittelpunkte der Umkreise der Dreiecke 
die Mittelpunkte
der Seiten des einbeschriebenen Quadrates (Thaleskreise).
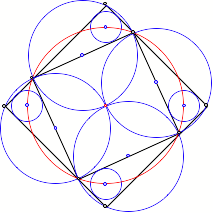
Quadrat
5.3
RegelmŠ§iges Sechseck
Die Mittelpunkte der
Umkreise der Dreiecke 
sind die
Schnittpunkte der beiden benachbarten Umkreise.
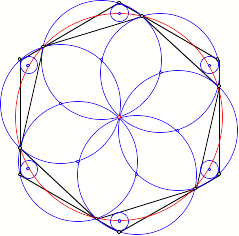
RegelmŠ§iges Sechseck
5.4
RegelmŠ§iges Siebeneck
†ber die Mittelpunkte
der Umkreise der Dreiecke 
kann nichts
ãSchšnesÒ gesagt werden.
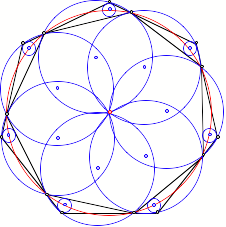
RegelmŠ§iges Siebeneck
Wir zeichnen nun aber
im einbeschriebenen Siebeneck sŠmtliche Diagonalen ein und sehen, dass jede
Diagonale durch genau vier Schnittpunkte von Umkreisen der Dreiecke 
verlŠuft. Warum
ist das so? Gibt es Entsprechendes bei anderen Eckenzahlen?
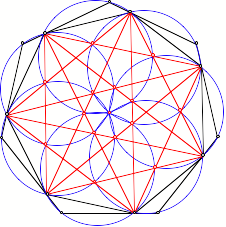
Diagonalen