Hans Walser, [20201012]

Vielecke verdoppeln

1 Worum geht es?

Regelmäßige Vielecke werden auf eine systematische Art flächenmäßig verdoppelt. Zerlegungsbeweis.

2 Bildergalerie

Zerlegung der regelmäßigen n-Ecke für n = 3, ... , 8.

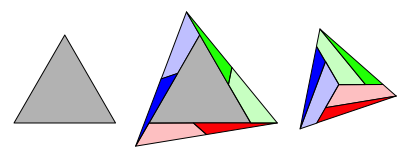
Abb. 1: Dreieckverdoppelung

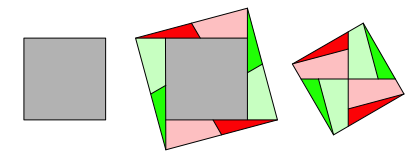
Abb. 2: Quadratverdoppelung

Das Quadrat lässt sich auch einfacher verdoppeln (Abb. 3).

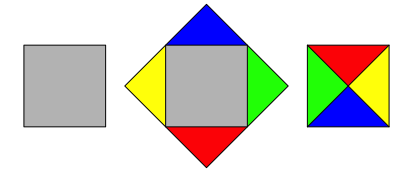
Abb. 3: Einfachere Quadratverdoppelung

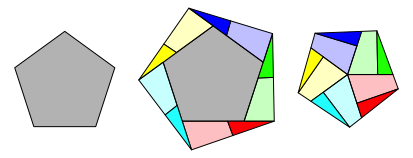
Abb. 4: Fünfeckverdoppelung

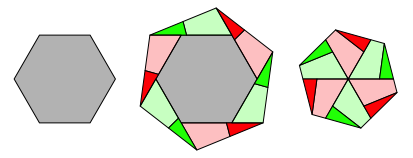
Abb. 5: Sechseckverdoppelung

Bei der Sechseckverdoppelung tritt der Goldene Schnitt auf (Walser 2013a). Die drei roten Punkte in der Abbildung 6 unterteilen die Strecke im Teilverhältnis des Goldenen Schnittes. Das ist überraschend. Den Goldenen Schnitt hätte man eher beim regelmäßigen Fünfeck erwartet.

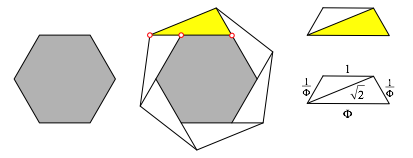
Abb. 6: Goldener Schnitt und Goldenes Trapez

Das gelbe Dreieck lässt sich zu einem der beiden Goldenen Trapeze ergänzen. Es ist gleichschenklig mit Basiswinkeln 60° und hat der Reihe nach die Seiten . Dabei ist

der numerische Wert des Goldenen Schnittes.

Interessanterweise haben die beiden Diagonalen die Länge , die man nicht im Kontext des Goldenen Schnittes vermuten würde. Die Zahl ist die Schlüsselzahl des DIN-Formates (Walser 2013b). In unserem Beispiel erscheint die Zahl wegen der Flächenverdoppelung.

Abb. 7: Siebeneckverdoppelung

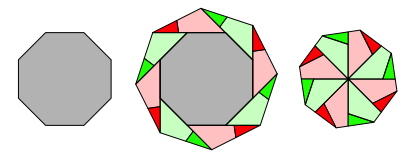
Abb. 8: Achteckverdoppelung

3 Konstruktionsvorgang

Wir beschreiben den Konstruktionsvorgang am Beispiel des regelmäßigen Fünfeckes (Abb. 4). Zunächst verlängern wir die Seiten des Fünfeckes zyklisch und zeichnen den Umkreis (Abb. 9).

Abb. 9: Verlängern und Umkreis

Nun vergrößern wir den Umkreis mit dem Längenfaktor und erhalten so ein entsprechend vergrößertes Fünfeck (Abb. 10). Dieses ist flächenmäßig doppelt so groß wie das Startfünfeck.

Abb. 10: Vergrößertes Fünfeck

Die Konstruktion erinnert bei entsprechender Einfärbung der beiden Kreise an den Euro (Abb. 11).

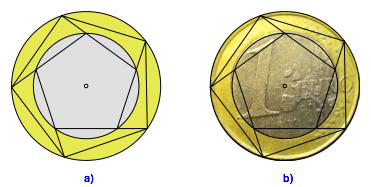
Abb. 11: Konstruktion im Euro

Das Fünfeck haben wir nun, es fehlt noch die Zerlegung. Die angesetzten leicht golden eingefärbten Dreiecke der Abbildung 12a haben einen Winkel von 72°. Sie lassen sich also zu einem Stern zusammensetzen (Abb. 12b). Dieser Stern hat denselben Flächeninhalt wie das Startfünfeck.

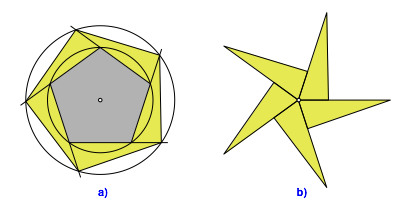
Abb.12: Stern

Wir müssen also den Stern in ein flächengleiches Fünfeck verwandeln. Dazu verbinden wir die Mittelpunkte derjenigen Sternkanten, die nicht in das Sternzentrum einmünden (Abb. 13a). Wir erhalten so ein regelmäßiges Fünfeck. Die vorstehenden Sternspitzen passen spiegelbildlich in die Lücken. Wir haben eine „Schmetterlingssymmetrie“ (Abb. 13b). So erhalten wir die Zerlegung der Abbildung 4. Die Stimmigkeit dieser Konstruktion ergibt sich aus dem Hilfssatz 1.

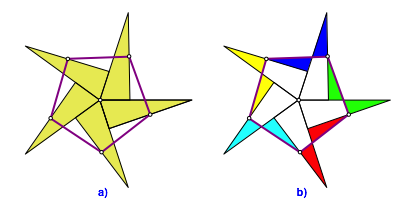
Abb.13: Abschneiden und ansetzen. Schmetterlinge

Literatur

Walser, Hans (2013a): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wußing über populärwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.

Walser, Hans (2013b): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-69-1.

Websites

Hans Walser: Goldene Trapeze und Goldenes Sechseck

http://www.walser-h-m.ch/hans/Miniaturen/G/Goldene_Trapeze/Goldene_Trapeze.htm

Hans Walser: Hilfssatz 1

http://www.walser-h-m.ch/hans/Miniaturen/H/Hilfssatz1/Hilfssatz1.htm

Hans Walser: Regelmäßige Vielecke

http://www.walser-h-m.ch/hans/Miniaturen/R/Reg_Vielecke2/Reg_Vielecke2.htm