1 Die Auslegeordnung

Wir beginnen mit vier kongruenten rechtwinkligen Dreiecken, von denen zwei spiegelbildlich zu den beiden anderen sind (Abb.1).

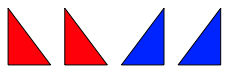
Abb. 1: Vier rechtwinklige Dreiecke

Diese ordnen wir nun an gemäß Abbildung 2.

Abb. 2: Umlegen der Dreiecke

Es entstehen zwei Rechtecke, in Umrissrechteck und ein „Lochrechteck“.

Wir vermuten, dass die beiden Rechtecke ähnlich sind.

Wir können die vier Dreiecke der Abbildung 1 noch auf eine zweite Art zu Rechtecken zusammenfügen (Abb. 3).

Abb. 3: Zweite Art

Wir vermuten wiederum, dass Umrissrechteck und Lochrechteck ähnlich sind.

2 Beweis

Wir verwenden die Bezeichnungen der Abbildung 4.

Abb. 4: Bezeichnungen

Für das Umrissrechteck haben wir das Seitenverhältnis (c + b) : a, für das Lochrechteck das Seitenverhältnis a : (c – b). Die Ähnlichkeitsbedingung ist:

Dies führt zu , also der Formel von Pythagoras, die in einem rechtwinkligen Dreieck erfüllt ist.

3 Sonderfälle

Wir diskutieren die Situation mit speziellen rechtwinkligen Dreiecken. Dazu normieren wir a =1, so dass wir nur noch den Parameter b im Spiel haben.

3.1 Goldenes Rechteck

Für ergibt sich die Situation der Abbildung 5. Wir erhalten das so genannte Goldene Rechteck, dessen Seitenlängen im Verhältnis des Goldenen Schnittes stehen.

Abb. 5: Goldenes Rechteck

Das Goldene Rechteck hat die Eigenschaft, dass nach Abschneiden eines Quadrates kleineres Goldenes Rechteck als Restrechteck übrig bleibt. Dies kann in unserem Beispiel durch eine andere Anordnung der Teilfiguren gezeigt werden (Abb. 6).

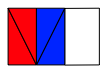
Abb. 6: Abschneiden eines Quadrates

3.2 Silbernes Rechteck

Für b = 1 erhalten wir das Rechteck der Abbildung 7, das Rechteck mit dem leicht esoterischen Namen Silbernes Rechteck. Es hat die Eigenschaft, dass nach Abschneiden von zwei Quadraten ein zum Ausgangsrechteck ähnliches Rechteck übrig bleibt.

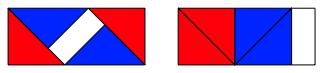
Abb. 7: Silbernes Rechteck

3.3 Allgemeiner Sonderfall

Für ergibt sich ein Rechteck mit der Eigenschaft, dass nach Abschneiden von n Quadraten ein zum Ausgangsrechteck ähnliches Rechteck übrig bleibt. Die Abbildung 8 illustriert den Fall für n = 5.

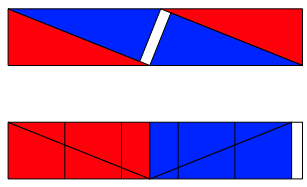
Abb. 8: n = 5

Für die Länge x des Rechteckes (bei einer Breite von 1) erhalten wir:

Dies führt zur positiven Lösung:

4 Umkehrung

Umgekehrt kann jedes Rechteck so zerlegt werden, dass vier kongruente rechtwinklige Dreiecke und ein zum Ausgangsrechteck ähnliches Rechteck entstehen. Dazu passen wir in das Rechteck zunächst einen Rhombus ein, dessen lange Diagonale mit einer der beiden Rechtecks-Diagonalen übereinstimmt. Die Abbildung 9 illustriert das weitere Vorgehen.

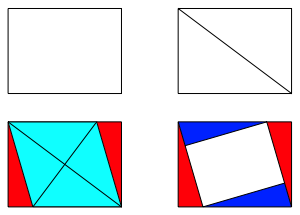
Abb. 9: Zerlegung eines Rechteckes