Hans Walser, [20161122]

Viereck-Viertelung

Anregung: Heinz Klaus Strick, Leverkusen

1 Eine Eigenschaft des Vierecks

Lehrsatz von D. Brune (Brune 1841): „Wenn man in einem Vierecke mit jeder der beiden Diagonalen durch den Mittelpunkt der andern eine Parallele zieht und den Durchschnittspunct dieser Parallelen mit den Mittelpuncten der vier Seiten durch gerade Linien verbindet, so theilen letztere das Viereck in vier flächengleiche Theile.“

2 Beweis

Die Situation affin invariant.

Wir transformieren das Viereck mit einer affinen Abbildung, welche das Seitenmittenparallelogramm auf das Einheitsquadrat abbildet (Abb. 1). Das Viereck hat nun orthogonale Diagonalen der Länge 2 und damit den Flächeninhalt 2. Jedes Teilviereck gemäß Konstruktion des Lehrsatzes hat eine Quadratseite der Länge 1 als Diagonale. Diese teilt das Teilviereck in zwei Dreiecke mit dieser gemeinsamen Grundlinie 1. Die zugehörigen Höhen ergänzen sich auf 1. Die Flächen der beiden Dreiecke ergänzen sich somit auf ½. Jedes Teilviereck hat also den Flächeninhalt ½. Dies ist ein Viertel des Flächeninhaltes des gesamten Ausgangsviereckes. Dies war zu beweisen.

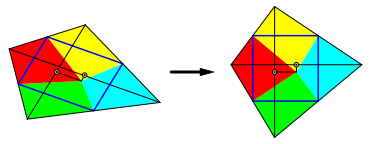
Abb. 1: Affine Transformation

3 Parkettierung

Die Abbildung 2 zeigt die übliche Parkettierung mit dem Ausgangsviereck der Abbildung 1.

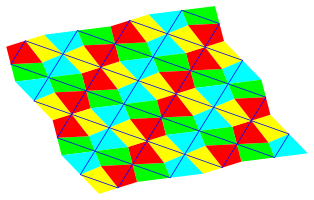
Abb. 2: Parkettierung

Literatur

Brune, D. (1841): Eine Eigenschaft des Vierecks. Journal für die reine und angewandte Mathematik. 22. S. 379.