Hans Walser, [20161123]
Viereck-Viertelung
Anregung: Heinz Klaus Strick, Leverkusen
1 Problemstellung
Welche Vierecke lassen sich von einem inneren Punkt aus mit geraden Verbindungen zu den vier Ecken in vier flchengleiche Dreiecke zerlegen?
Triviale Lsungen sind Quadrat, Rechteck, Rhombus oder allgemein Parallelogramm mit dem Diagonalenschnittpunkt als innerem Punkt. Eine weitere Lsung ist das Drachenviereck mit dem Mittelpunkt der Symmetrieachse als innerem Punkt.
2 Der schiefe Drachen
Unter einem schiefen Drachenviereck verstehe ich ein affines Bild eines Drachenvierecks (Abb. 1). Eine der beiden Diagonalen wird durch die andere Diagonale halbiert.

Abb. 1: Schiefer Drachen
Ein schiefer Drachen kann ausgehend vom Mittelpunkt derjenigen Diagonalen, welche die andere Diagonale halbiert, in vier flchengleiche Dreiecke zerlegt werden (Abb. 1b).
Die oben erwhnten trivialen Lsungen sind Sonderflle von schiefen Drachen.
Wir werden sehen, dass das auch schon alles ist.
3 Theorem
Ein Viereck lsst sich genau dann von einem inneren Punkt aus mit geraden Verbindungen zu den vier Ecken in vier flchengleiche Dreiecke zerlegen, wenn es ein schiefes Drachenviereck ist.
Der Beweis in der einen Richtung ist einfach. Die vier Dreiecke in der Abbildung 1b haben gleich lange Grundlinien und gleich lange Hhen.
Fr die andere Richtung ist zu zeigen: Ein Viereck, das von einem inneren Punkt aus mit geraden Verbindungen zu den vier Ecken in vier flchengleiche Dreiecke zerlegt werden kann, ist ein schiefes Drachenviereck. Dazu mchte ich etwas weiter ausholen.
4 Affine Invarianz
Die in unserem Theorem vorkommenden Begriffe und Methoden sind affin invariant.
Wir knnen daher ein beliebiges Viereck durch eine affine Abbildung in eine Standardsituation bringen wie folgt. Das Seitenmittenparallelogramm soll auf ein Quadrat der Seitenlnge 1 abgebildet werden.
Die beiden Diagonalen stehen dann orthogonal aufeinander und haben je die Lnge 2. Das Viereck hat daher den Flcheninhalt 2.
Wir
passen ein kartesisches Koordinatensystem mit den Achsen auf den beiden Diagonalen
ein. Es sei ![]() der
Mittelpunkt der Diagonalen AC und
der
Mittelpunkt der Diagonalen AC und ![]() der Mittelpunkt
der Diagonalen BD. Wegen der
Diagonalenlnge 2 erhalten wir die Situation der Abbildung 2.
der Mittelpunkt
der Diagonalen BD. Wegen der
Diagonalenlnge 2 erhalten wir die Situation der Abbildung 2.

Abb. 2: Standardisierte Situation im Koordinatensystem
5 Flchenberechnungen
Da das ganze Viereck den Flcheninhalt 2 hat, mssen die Teildreiecke bei Flchengleichheit je den Flcheninhalt ½ haben.
Wir
whlen nun einen Punkt ![]() im Innern
des Viereckes ABCD und berechnen
formal die Flcheninhalte der Teildreiecke.
im Innern
des Viereckes ABCD und berechnen
formal die Flcheninhalte der Teildreiecke.
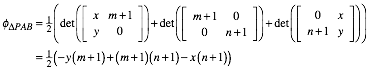 (1)
(1)
Analog:
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
Die Flcheninhalte der Teildreiecke hngen linear von x und y ab.
Wir
suchen eigentlich Punkte ![]() , fr welche die vier Flcheninhalte (1) bis (4)
gleich sind. Vorerst aber ein etwas einfacheres Problem.
, fr welche die vier Flcheninhalte (1) bis (4)
gleich sind. Vorerst aber ein etwas einfacheres Problem.
6 Alternierende Flchensumme null
Wir
suchen vorerst Punkte ![]() fr welche
gilt:
fr welche
gilt:
![]() (5)
(5)
Einsetzen von (1) bis (4) in (5) gibt:
![]() (6)
(6)
Das ist
die Gleichung der Geraden g, welche
durch ![]() und
und ![]() verluft.
verluft.
Fr einen beliebigen Punkt P auf dieser Geraden g erhalten wir also vier Dreiecke, deren alternierende Flchensumme verschwindet. Das gilt nicht nur im standardisierten Fall sondern auch im allgemeinen Viereck (Abb. 3). Die Flchensumme der roten Dreiecke ist gleich der Flchensumme der hellblauen Dreiecke.
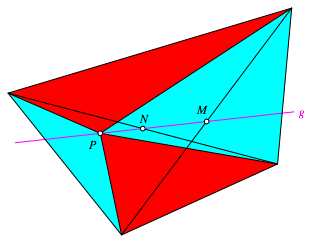
Abb. 3: Rot = Hellblau
Dieses Resultat ist der Satz von Anne (Humenberger und Schuppar 2016). Die Gerade g wird als Newtongerade bezeichnet.
Der Satz von Anne liefert zwar nicht vier flchengleiche Teildreiecke, aber immerhin zwei Paare je gegenberliegender Teildreiecke, deren paarweisen Flchensummen gleich sind.
Das hei§t aber, dass fr unsere Fragestellung nach vier flchengleichen Teildreiecken der Punkt P, falls er berhaupt existiert, auf der Geraden g liegen muss.
7 Flchengleiche Teildreiecke
Aus der Bedingung
![]() (7)
(7)
erhalten wir durch Einsetzen von (1) und (2):
![]() (8)
(8)
Subtraktion von (6) liefert:
![]() (9)
(9)
Wir machen nun eine Fallunterscheidung bezglich m.
Erster
Fall: ![]()
In diesem
Fall ist wegen (6) ![]() , das hei§t P
= M. Wegen
, das hei§t P
= M. Wegen ![]() erhalten
wir durch Einsetzen der Werte x = m und y = 0 in (1) die Bedingung n
= 0. Der Punkt N ist also der
Ursprung und das standardisierte Viereck ABCD
ein Drachenviereck mit der x-Achse
als Symmetrieachse. Das ursprngliche Viereck ist ein schiefes Drachenviereck.
erhalten
wir durch Einsetzen der Werte x = m und y = 0 in (1) die Bedingung n
= 0. Der Punkt N ist also der
Ursprung und das standardisierte Viereck ABCD
ein Drachenviereck mit der x-Achse
als Symmetrieachse. Das ursprngliche Viereck ist ein schiefes Drachenviereck.
Zweiter Fall: m = 0
Der Punkt M ist der Ursprung. Wegen (9) ist x = 0 und wegen (6) y = n, das hei§t P = N. Das standardisierte Viereck ist ein Drachenviereck mit der y-Achse als Symmetrieachse, das ursprngliche Viereck ein schiefes Drachenviereck.
Damit ist das Theorem in beiden Richtungen bewiesen.
Literatur
Humenberger, Hans und Schuppar, Berthold
(2016): Flchenausgleich bei Wei§ und Grau in Vierecken – der Satz von Anne und sein Umfeld. MU, Der Mathematikunterricht.
Jahrgang 62. Heft 5-2016. S. 26-36.