Hans Walser, [20120528]

Viereck

Es werden einige Spielereien am Viereck untersucht. Daraus ergeben sich interessante Eigenschaften für spezielle Vierecke, die im üblichen Kanon des Hauses der Vierecke nicht enthalten sind.

1 Viereck und halbe Quadrate

1.1 Die Figur

Wir setzen einem beliebigen Viereck auf den Seiten halbe Quadrate in Form gleichschenklig rechtwinkliger Dreiecke an gemäß Abbildung 1.

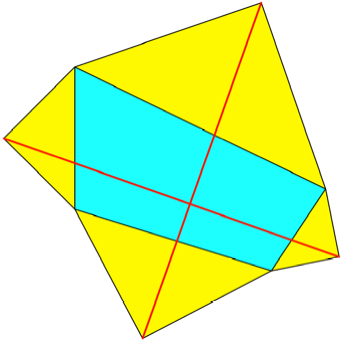
Abb. 1: Viereck mit aufgesetzten halben Quadraten

Dann sind die beiden roten Strecken gleich lang und orthogonal.

1.2 Der Beweis

Wir bearbeiten einen allgemeinen Fall, indem wir den Vierecksseiten ähnliche gleichschenklige Dreiecke aufsetzen. Die roten Strecken sind dann weder gleich lang noch orthogonal.

Für den Beweis arbeiten wir mit Vektoren gemäß Abbildung 2.

Die Indizes sind mod 3 zu rechnen.

Es seien die Seitenvektoren und die um gedrehten Vektoren .

Die beiden Diagonalvektoren bezeichnen wir mit und .

Weiter sei . In der Abbildung 1 ist (die Vektoren schauen nach innen), in der Abbildung 2 ist .

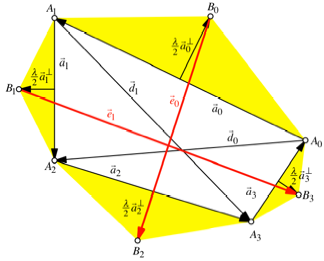
Abb. 2: Bezeichnungsfigur

Die für unsere Überlegungen relevanten Vektoren sind und .

Mit einiger Rechnung erhalten wir:

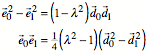
Daraus ergibt sich: Für sind die beiden Vektoren , und damit die roten Strecken gleich lang und orthogonal. Die Abbildung 1 gehört zum Fall . Für müssen wir die Dreiecke nach innen ansetzen, wobei sie sich teilweise überlappen (Abb. 3).

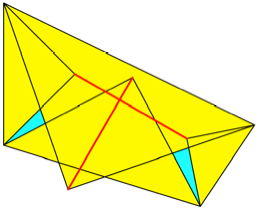
Abb. 3: Halbe Quadrate nach innen

Die Abbildung 4 zeigt die Überlagerung der Abbildungen 1 und 3. Diese Figur lässt auch eine Interpretation als Gelenkmodell zu: Vier Quadrate werden an je gegenüberliegenden Ecken gelenkig zu einer geschlossenen Figur verbunden. Die restlichen Quadratecken können zu zwei orthogonalen Kreuzen mit je gleich langen Kreuzbalken verbunden werden.

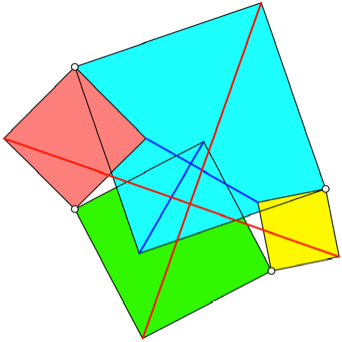
Abb. 4: Gelenkmodell

2 Spezielle Vierecke

Wir haben gesehen, dass in einem beliebigen Viereck die Beziehungen gelten:

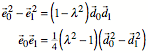
Damit drängen sich Sonderfälle von Vierecken auf, in denen die Diagonalen entweder senkrecht oder gleich lang oder beides sind.

2.1 Orthogonale Diagonalen

Aus der Beziehung

folgt, dass die beiden roten Strecken gleich lang sind (Abb. 5).

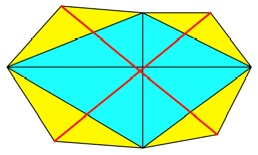
Abb. 5: Orthogonale Diagonalen

Die roten Strecken sind nicht mehr orthogonal, aber wir sehen, dass ihre Richtungen spiegelbildlich zu den Diagonalen liegen.

Für den Beweis setzen wir die Diagonalen auf die Koordinatenachsen und verwenden die Eckpunktskoordinaten:

Damit erhalten wir:

Daraus lässt sich die Spiegelbildlichkeit der Richtungen ablesen.

2.1.1 Sonderfall: Verbindungen gegenüberliegender Kantenmitten

Für erhalten wir die Verbindungen der Kantenmitten. Diese sind somit gleich lang und liegen richtungsmäßig spiegelbildlich zu den Diagonalen. Dies ist allerdings nicht so umwerfend, weil diese Verbindungen ihrerseits die Diagonalen des Kantenmittenparallelogramms sind, welches in unserem Fall ein Rechteck ist (Abb. 6).

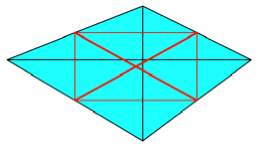
Abb. 6: Kantenmittenrechteck

2.1.2 Sonderfall: Halbe Quadrate

Für erhalten wir wie oben halbe aufgesetzte Quadrate. Die roten Strecken sind orthogonal. Wir sehen, dass sie sich im Diagonalenschnittpunkt schneiden.

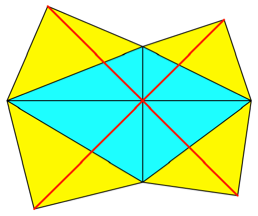
Abb. 7: Kopunktale Geraden

Uff, auch das möchten die Schulmeister bewiesen haben. Für die Koordinatendisposition

erhalten wir:

Diese Punkte liegen auf den Geraden .

2.2 Gleich lange Diagonalen

Aus

ergibt sich, dass die roten Strecken orthogonal sind.

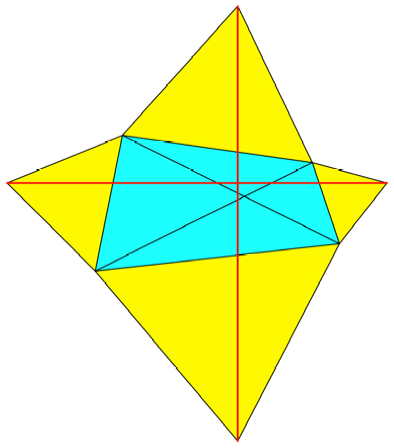
Abb. 8: Gleich lange Diagonalen

Nun sind die Richtungen der Diagonalen spiegelbildlich zu den Richtungen der roten Strecken. Das war ja zu erwarten, daher habe ich die Diagonalen mit symmetrischen Richtungen zu den Achsen disponiert. Mit der Koordinatendisposition

ergibt sich diese symmetrische Disposition. Wir erhalten:

Diese Vektoren stehen waagerecht und senkrecht.

2.3 Dualität

Die Vierecke mit orthogonalen Diagonalen und die Vierecke mit gleich langen Diagonalen verhalten sich dual zu einander. Das Aufsetzen von gleichschenkligen Dreiecken bei einem Typ führt jeweils zum anderen Typ. Es sind jeweils nur die Diagonalen gezeichnet, die Vierecke selber fehlen.

Das einfachste Beispiel zu dieser Dualität sind Rhombus und Rechteck. Das nächste Beispiel sind Drachenviereck und gleichschenkliges Trapez.

2.3.1 Iteration

Die Abbildung 9 zeigt ein iteratives Aufsetzen von gleichschenkligen Dreiecken. Die schwarz gezeichneten Diagonalen sind jeweils orthogonal, die roten gleich lang.

Wir sehen, dass in diesem Beispiel mit der Zeit nicht konvexe Vierecke entstehen. Die Sache läuft aus dem Ruder.

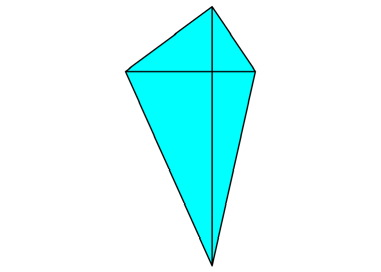
Abb. 9a: Ausgangsviereck mit orthogonalen Diagonalen

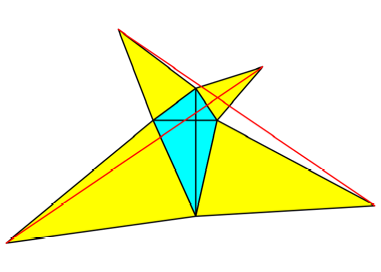
Abb. 9b: Erster Schritt: Viereck mit gleich langen Diagonalen

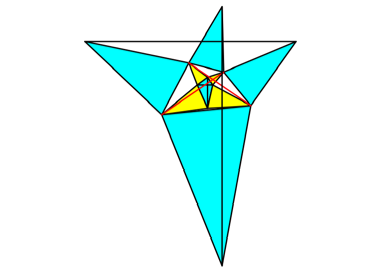
Abb. 9c: Zweiter Schritt: Viereck mit orthogonalen Diagonalen

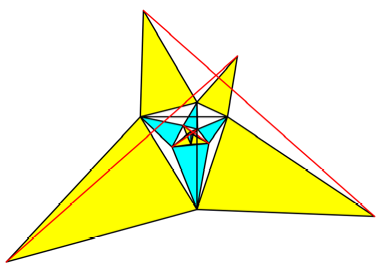
Abb. 9d: Dritter Schritt

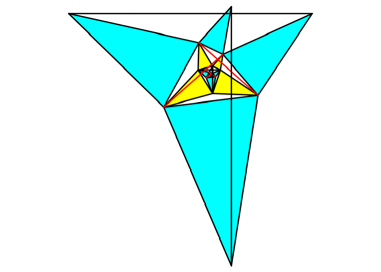
Abb. 9e: Vierter Schritt

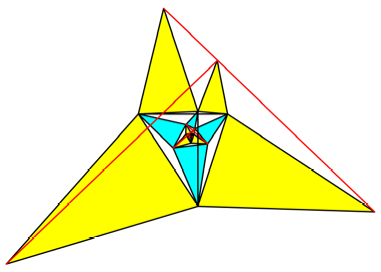
Abb. 9f: Fünfter Schritt. Viereck nicht mehr konvex

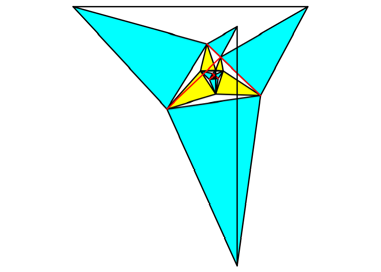
Abb. 9g: Sechster Schritt

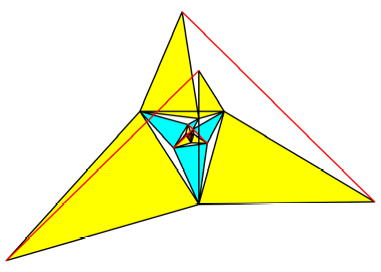
Abb. 9h: Siebenter Schritt

2.3.2 Selbstdualität

Wenn wir halbe Quadrate aufsetzen, entsteht als Limesfigur ein Quadrat (Abb. 10). Die Dreiecke überlappen sich teilweise.

Die Diagonalen sind jeweils orthogonal. Mit Ausnahme der Startfigur haben alle Vierecke auch gleich lange Diagonalen. Die Figuren sind selbstdual. Das einfachste Beispiel dazu ist das Quadrat.

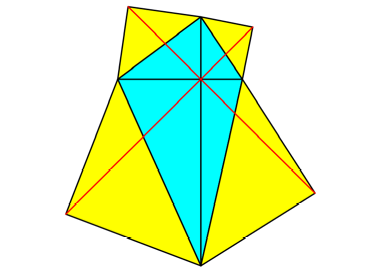
Abb. 10a: Erster Schritt

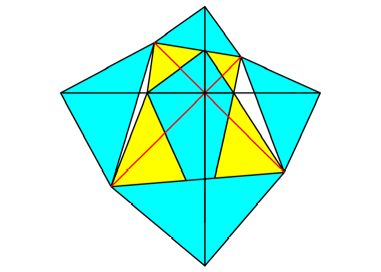
Abb. 10b: Zweiter Schritt. Überlappung

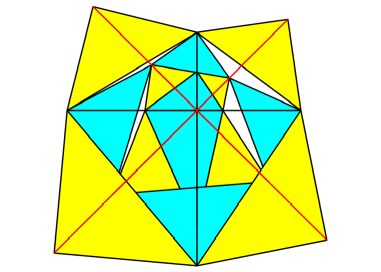
Abb. 10c: Dritter Schritt

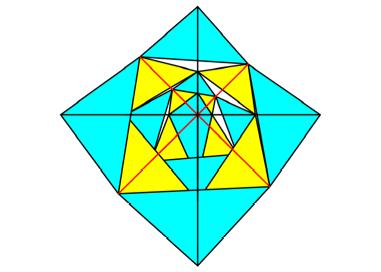
Abb. 10d: Vierter Schritt

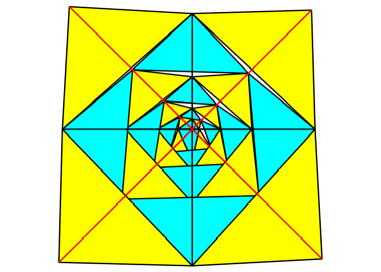
Abb. 10e: Siebenter Schritt

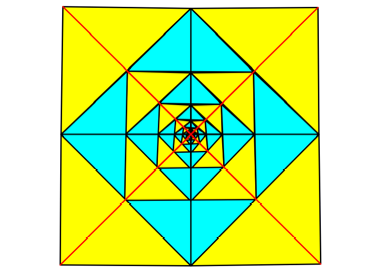
Abb. 10f: Elfter Schritt. Beinahe ein Quadrat