Hans Walser, [20210716]
Viereck
1 Worum geht es?
Eine Schließungsfigur mit vier ähnlichen Vierecken (Abb. 1). Spiel mit weiteren ähnlichen Vierecken.

Abb. 1: Schließungsfigur
2 Vorgehen
Wir beginnen mit einem beliebigen Viereck A1B1C1D1 (Abb. 2.1).

Abb. 2.1: Startviereck
Wir nehmen nun ein zweites, zum ersten ähnliches Viereck A2B2C2D2 und setzen die Ecke A2 in die Ecke C1 des ersten Viereckes an (Abb. 2.2). Die beiden Vierecke können an diesem gemeinsamen Gelenkpunkt beliebig verdreht werden.

Abb. 2.2: Ansetzen eines zweiten Vierecks
Nun spannen wir ein drittes, ebenfalls ähnliches Viereck A3B3C3D3 so ein, dass A3 = B1 und C3 = B2 (blau in Abb. 2.3). Dieses Viereck ist vollständig bestimmt.
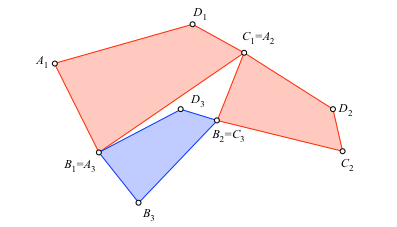
Abb. 2.3: Einspannen eines dritten Vierecks
Schließlich spannen wir ein viertes ähnliches Viereck A4B4C4D4 so ein, dass A4 = D1 und C4 = D2 (Abb. 2.4). Auch dieses Viereck ist vollständig bestimmt.

Abb. 2.4: Einspannen eines vierten Viereckes. Schließungsfigur
3 Schließungsfigur
Nun ist B4 = D3. Wir haben eine Schließungsfigur.
Die Schließungsfigur ist struktursymmetrisch. Wir hätten auch mit den blauen Vierecken beginnen können.
4 Nachweis der Schließungseigenschaft
Wir arbeiten in der Ebene der komplexen Zahlen. Es sei xi die zu Xi gehörende Zahl. Gegeben sind zunächst die zum ersten Viereck gehörenden Zahlen a1, b1, c1 und d1. Ebenfalls gegeben ist die komplexe Zahl l, der Ähnlichkeitsfaktor, um vom ersten Viereck zum zweiten zu kommen. Der Betrag von l beschreibt den reellen Ähnlichkeitsfaktor, das Argument von l die Verdrehung. Damit lassen sich alle restlichen Daten bestimmen. Es ist:
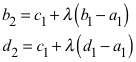 (1)
(1)
Weiter sind
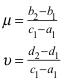 (2)
(2)
die komplexen Ähnlichkeitsfaktoren zwischen dem dritten Viereck und dem ersten Viereck beziehungsweise zwischen dem vierten Viereck und dem ersten Viereck. Damit wird:
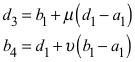 (3)
(3)
Zu zeigen ist d3 = b4. Dies folgt mit einiger Rechnung durch Einsetzen von (1) und (2) in (3).
5 Beispiele
5.1 Nicht konvexes Viereck
Die Schließungseigenschaft gilt auch für nicht konvexe Vierecke (Abb. 3).

Abb. 3: Nicht konvexes Viereck
5.2 Überschlagenes Viereck
Die Schließungseigenschaft gilt auch bei „überschlagenen“ Vierecken (Abb. 4 mit angepasster Färbung).

Abb. 4: Überschlagenes Viereck
5.3 Spezielle Punkte im Viereck
Wir nehmen in jedem der vier Vierecke einen besonderen Punkt und bilden das Viereck dieser Punkte.
5.3.1 Diagonalenschnittpunkte
Wir zeichnen in jedem der vier Vierecke den Diagonalenschnittpunkt. Das Viereck der vier Diagonalenschnittpunkte ist ebenfalls ähnlich zu den vier Vierecken (Abb. 5).
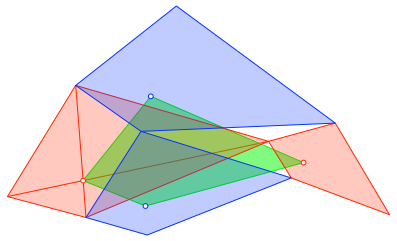
Abb. 5: Diagonalenschnittpunkte-Viereck
5.3.2 Eckenschwerpunkte
Ein Viereck hat verschiedene Schwerpunkte. Die Vorstellung beim Eckenschwerpunkt ist eine gleichmäßige Verteilung der Gesamtmasse in den vier Ecken. Die Vorstellung beim Kantenschwerpunkt ist eine Verteilung der Gesamtmasse auf vier Kanten im Verhältnis ihrer Länge. Diesen Schwerpunkt habe ich nicht untersucht. Die Vorstellung dem Flächenschwerpunkt ist eine homogene Massenverteilung auf der Fläche.
Wir zeichnen in jedem der vier Vierecke den Eckenschwerpunkt. Das Viereck der vier Eckenschwerpunkte ist ebenfalls ähnlich zu den vier Vierecken (Abb. 6).
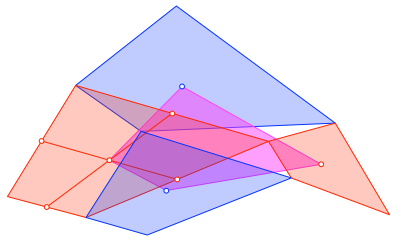
Abb. 6: Eckenschwerpunkte-Viereck
5.3.3 Flächenschwerpunkte
Wir zeichnen in jedem der vier Vierecke den Flächenschwerpunkt. Das Viereck der vier Flächenschwerpunkte ist ebenfalls ähnlich zu den vier Vierecken (Abb. 7).
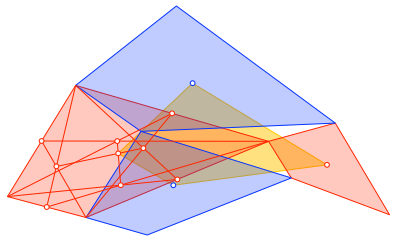
Abb. 7: Flächenschwerpunkte-Viereck
Die Abbildung 8 ist eine Überlagerung der Abbildungen 5, 6 und 7.
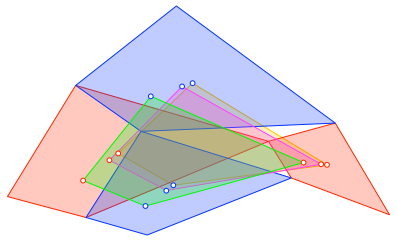
Abb. 8: Überlagerung
Die speziellen Punkte sind verschieden. Sie liegen aber jeweils auf einer Geraden und haben das Teilverhältnis 3:1.
Websites
Hans Walser: Schwerpunkte im Viereck
http://www.walser-h-m.ch/hans/Miniaturen/S/Schwerpunkte_Viereck/Schwerpunkte_Viereck.htm