Hans Walser, [20191101]
Viereckspiralen
1 Worum geht es?
Spiralen auf der Basis eines unregelmŠ§igen Vierecks.
2 Die beiden Spiralen
Wir beginnen mit einem unregelmŠ§igen Viereck (Abb. 1). Das Viereck ist zwar unregelmŠ§ig, aber nicht beliebig. Wir kommen spŠter darauf zurźck.

Abb. 1: Viereck
Dem Viereck fźgen wir ein zweites von gleicher Form an (Abb. 2).

Abb. 2: Zweites Viereck
Das zweite (blaue) Viereck ist gegenźber dem ersten verkleinert. Der LŠngen-VerŠnderungsfaktor ist das VerhŠltnis der LŠnge der Seite links unten zur LŠnge der Seite rechts oben im ersten (roten) Viereck. Zudem ist das zweite Viereck gegenźber dem ersten verdreht. Der Drehwinkel ist der Winkel zwischen der Seite rechts oben und der Seite rechts unten im ersten (roten) Viereck. Das zweite Viereck geht also aus dem ersten Viereck durch eine Drehstreckung hervor.
Nun fźgen wir nach dem gleichen Verfahren ein weiteres Viereck an (Abb. 3).

Abb. 3: Drittes Viereck
Wenn wir so weiterfahren, entsteht eine eckige Spirale (Abb. 4). Da wir mit Drehstreckungen arbeiten, handelt es sich um eine logarithmische Spirale.

Abb. 4: Spirale
Wir kšnnen allerdings dem Startviereck der Abbildung 1 auch oben ein Viereck von gleicher Form anfźgen (Abb. 5).

Abb. 5: Zweites Viereck oben angefźgt
Wenn wir entsprechend weiterfahren, erhalten wir ebenfalls eine Spirale (Abb. 6).

Abb. 6: Die andere Spirale
3 †berlagerung der beiden Spiralen
Die beiden Spiralen haben das gleiche Startviereck. Wenn wir sie źberlagern, ergibt sich die Figur der Abbildung 7.

Abb. 7: Die beiden Spiralen
Wir stellen etwas Verblźffendes fest. Die beiden Spiralen treffen sich wieder und wieder und wieder ... . Und zwar kommen wir nach sechs Schritten auf der einen Spirale zum selben Viereck wie nach zwšlf Schritten auf der anderen Spirale. Dieses zweite gemeinsame Viereck spielt nun dieselbe Rolle wie das gemeinsame Startviereck. Die innere Schlaufe ist also eine verkleinerte Kopie der Gesamtfigur. Wir erkennen noch zwei weitere solche Schlaufen. Im Prinzip sind es unendlich viele Schlaufen.
Das ist allerdings nicht bei jedem beliebigen Startviereck so. In der Regel źberschneiden sich die beiden Spiralen nicht passend in einem gemeinsamen Viereck. Wir zeigen unten, wie das gemacht wurde.
4 Noch mehr Spiralen
Da alle Vierecke in der Abbildung 7 dieselbe Form haben, kšnnen wir jedes dieser Vierecke als Startviereck verwenden. So kšnnen wir etwa ausgehend vom zweiten Viereck (blau) in der unteren Spirale eine weitere Spirale nach oben starten. Diese źberschneidet die untere Spirale ebenfalls in einem gemeinsamen Viereck.
Wir kšnnen daher die Ebene kohŠrent mit Spiralen fźllen. Die Abbildung 8 illustriert einen Ausschnitt, begrenzt durch die beiden Startspiralen.

Abb. 8: Auffźllen mit Spiralen
Die Abbildung 9 zeigt einen zentralen Ausschnitt.

Abb. 9: Ausschnitt
Wir erkennen jetzt noch weitere Spiralen, gebildet durch Vierecke, welche źbereck aneinandergefźgt sind.
5 Wie es gemacht wird
Wir
arbeiten mit einem im Prinzip unendlich langen Streifen in einem
Parallelogramm-Punktraster (Abb. 10). Ein vertikaler
Schnitt durch den Streifen muss die Hšhe ![]() haben.
Unterkante und Oberkante des Streifens mźssen bei einer Translation in der y-Richtung um
haben.
Unterkante und Oberkante des Streifens mźssen bei einer Translation in der y-Richtung um ![]() punktschlźssig aufeinander abbildbar
sein. Ansonsten sind wir in der Gestaltung des Streifens frei.
punktschlźssig aufeinander abbildbar
sein. Ansonsten sind wir in der Gestaltung des Streifens frei.
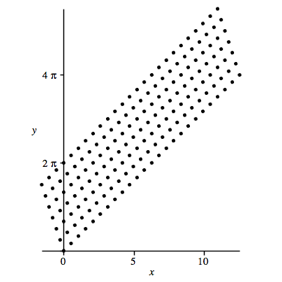
Abb. 10: Streifen im Punktraster
Wir
bilden nun den Streifen mit der komplexen Exponentialabbildung ![]() ab. Diese
hat die reelle Darstellung:
ab. Diese
hat die reelle Darstellung:
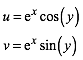 (1)
(1)
Wegen der
PeriodizitŠt der Funktionen Kosinus und Sinus in (1) mźssen wir beim Streifen
in der y-Richtung eine
†bereinstimmung nach einer Translation um ![]() haben.
haben.
Die Abbildung 11 zeigt einen zentralen Ausschnitt des Bildes.

Abb. 11: Bild des Punktrasters
Wir erkennen sowohl linkslŠufige wie auch rechtslŠufige Spiralen. Jeder Punkt liegt auf je einem dieser beiden Spiralentypen. Da wir mit der Exponentialfunktion abgebildet haben, handelt es sich um logarithmische Spiralen.
Die Abbildung 12 zeigt das Bild des fźr unsere †berlegungen verwendeten Punktrasters.
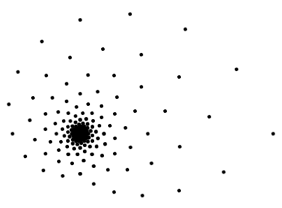
Abb. 12: Verwendeter Punktraster
Diese Punkte verbinden wir nun geradlinig zu Vierecken. Wir erkennen am rechten Bildrand der Abbildung 12 unser Startviereck.