Hans Walser, [20170516]

Viererpuzzle im Raum

1     Worum geht es?

Viererpuzzle in der Ebene sind Figuren mit folgender Eigenschaft: Vier gleichsinnig kongruente Kopien kšnnen zu einer Figur zusammengesetzt werden, welche zur Ausgangsfigur gleichsinnig Šhnlich ist.

Man kann es auch umgekehrt formulieren: Die Figur kann in vier gleichsinnig kongruente Teilfiguren zerlegt werden, die zur Ausgangsfigur gleichsinnig Šhnlich sind.

Die Abbildung 1 zeigt einige Beispiele.

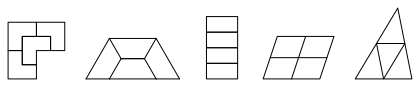
Abb. 1: Beispiele in der Ebene

Die Abbildung 2 zeigt Beispiele, wo es mit der Gleichsinnigkeit nicht stimmt. Die blau markierten Teilfiguren sind gleichsinnig Šhnlich zur Endfigur, die rot markierten ungleichsinnig.

Abb. 2: Ungleichsinnig

Oft wird auf die Gleichsinnigkeit verzichtet. Zu Viererpuzzles in der Ebene siehe (Hemme 1989).

Wir fragen nach Analoga im Raum.

2     Im Raum

Ich habe nur zwei Beispiele gefunden, die erst noch miteinander verwandt sind.

In den Beispielen treten folgende irrationale Schlźsselzahlen auf:

 

                                                                 (1)

2.1    Lineare Anordnung. Stapel

Die Abbildung 3a zeigt die Startfigur mit Verma§ung. Die Startfigur ist ein Quader mit dem SeitenverhŠltnis:

 

                                                                                     (2)

 

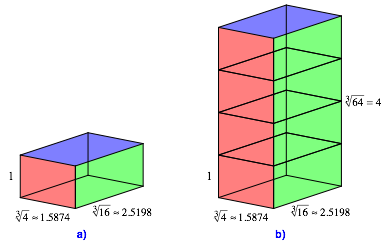
Abb. 3: Quader und Stapel

Die Abbildung 3b zeigt einen Stapel von vier solchen Quadern. Es ist ebenfalls ein Quader. Er hat das SeitenverhŠltnis:

 

                                                                               (3)

 

Die SeitenverhŠltnisse (2) und (3) stimmen źberein, wir haben von (2) zu (3) den Erweiterungsfaktor .

Die Abbildung 4a zeigt den umgelegten Stapel, die Abbildung 4b die mit dem Faktor  gestreckte Ausgangsfigur der Abbildung 3a. Wir sehen die €hnlichkeit und die zyklische Farbvertauschung. 

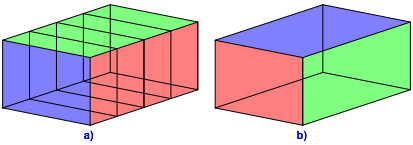
Abb. 4: €hnlichkeit

2.2    Doppelstapel

2.2.1   Viererpuzzle

Wegen 2 × 2 = 4 kšnnen wir versuchen, einen Stapel mit nur 2 Quadern nochmals zu stapeln. Die Ausgangsfigur der Abbildung 5a ist ein Quader mit dem SeitenverhŠltnis:

 

                                                                                       (4)

 

Dieser Quader hat also ein anderes Format als der Quader der Abbildung 3a.                    

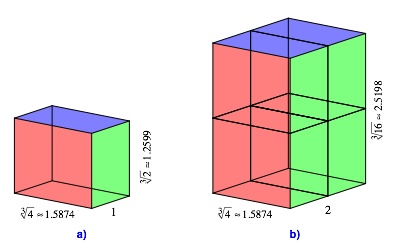
Abb. 5: Doppelstapel

Der Doppelstapel der Abbildung 5b ist ein Quader mit dem SeitenverhŠltnis:

 

                                                                                   (5)

 

Die SeitenverhŠltnisse (4) und (5) sind gleich, der Erweiterungsfaktor ist .

Die Abbildung 6a zeigt den umgelegten Stapel der Abbildung 5b, die Abbildung 6b den mit dem Faktor  gestreckten Ausgangsquader der Abbildung 5a. Wir sehen die €hnlichkeit und die zyklische Farbvertauschung.

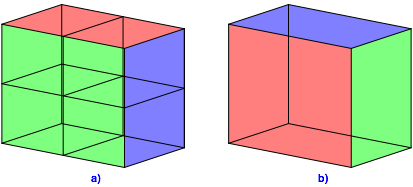
Abb. 6: €hnlichkeit

2.2.2   Link mit dem DIN-Format

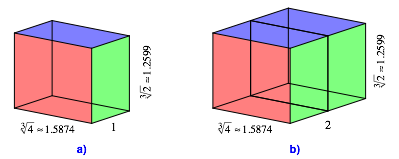
Abb. 7: Zweierpuzzle

Die Abbildung 7 zeigt die Situation der Abbildung 5 unter Weglassung der oberen HŠlfte beim Stapel.

Der Quader der Abbildung 7b hat das SeitenverhŠltnis:

 

                                                                                     (6)

 

Dies ist ebenfalls gleich dem SeitenverhŠltnis (4) (Erweiterungsfaktor ). Wir haben jetzt allerdings kein Viererpuzzle mehr, sondern nur noch ein Zweierpuzzle. Es handelt sich um das rŠumliche Analogon zum DIN-Format (Walser 2013, S. 55f).

 

Fźr Hinweise auf weitere Lšsungen bin ich dankbar.

 

Literatur

Hemme, Heinrich (1989): Geometrische Gerźchte: Figuren, die sich selbst vervielfachen. bild der wissenschaft, 5-1989. 141-144.

Walser, Hans (2013): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Edition am Gutenbergplatz, Leipzig 2013. ISBN 978-3-937219-69-1.