Hans Walser, [20161001]

Vierkreisepunkt

Anregung: G. Sch., G.

1 Der Schnittpunkt

Bei vier Geraden in allgemeiner Lage gibt es Möglichkeiten, drei Geraden auszuwählen und damit ein Dreieck zu bilden.

Die Umkreise dieser vier Dreiecke schneiden sich in einem Punkt (Abb. 1).

Abb. 1: Schnittpunkt von vier Kreisen

2 Beweis

2.1 Bezeichnungen

Wir verwenden die Bezeichnungen der Abbildung 2.

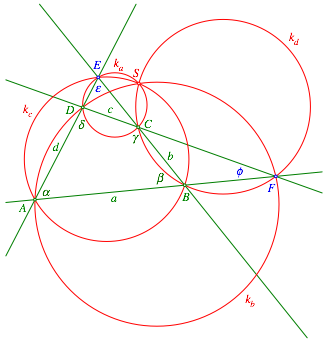
Abb. 2: Bezeichnungen

Es gelten folgende Winkelbeziehungen:

(1)

Zunächst sei S der Schnittpunkt der beiden Kreise k_a und k_b. Wir haben zu zeigen, dass auch die Kreise k_c und k_d durch S verlaufen.

2.2 k_c verläuft durch S

Wir überlegen anhand der Abbildung 3.

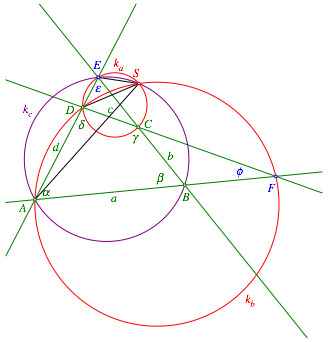
Abb. 3: Überlegung für den Kreis k_c

Wir verwenden die Kreise k_a und k_b als Ortsbogen für Peripheriewinkel. Es ist:

(2)

Daraus erhalten wir unter Verwendung von (1):

(3)

Damit liegt S auf dem Kreis k_c.

2.3 k_d verläuft durch S

Das ist jetzt aus logischen Symmetriegründen klar.

Wir können aber auch direkt überlegen (Abb. 4).

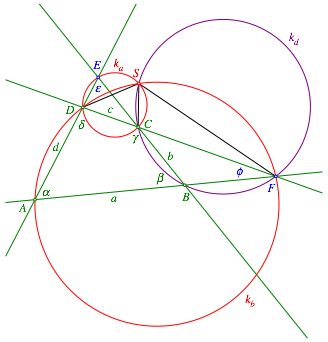
Abb. 4: Überlegung für den Kreis k_d

Es ist:

(4)

Daraus erhalten wir unter Verwendung von (1):

(5)

Damit liegt S auf dem Kreis k_d.

3 Fünfpunktekreis

In der Figur der Abbildung 1 zeichnen wir noch die Mittelpunkte der vier roten Umkreise ein. Diese liegen zusammen mit dem Schnittpunkt auf einem Kreis (Abb. 5).

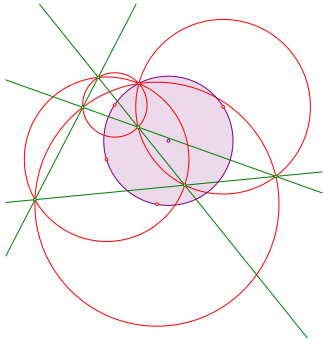
Abb. 5: Fünfpunktekreis

Für den Beweis benötigen wir den Satz von Wallace (Walser, Schlussgerade).

Website

Hans Walser: Schlussgerade (01.10.2016)

http://www.walser-h-m.ch/hans/Miniaturen/S/Schlussgerade/Schlussgerade.htm