Hans Walser, [20210418]

Vierteln regelmäßiger Vielecke

1 Worum geht es?

Wir zerlegen regelmäßige Vielecke gerader Eckenzahl in vier regelmäßige Vielecke der gleichen Eckenzahl. Für ungerade Eckenzahlen siehe hier.

Eine Fleißarbeit.

2 Beispiele

Die Figurenfolgen haben je eine eigene Systematik. Diese ist bei größeren Eckenzahlen leichter erkennbar.

2.1 Einstieg

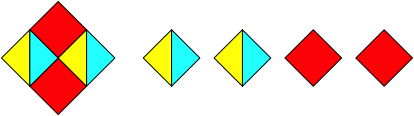
Abb. 1.4: Quadrat

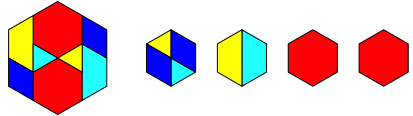
Abb. 1.6: Sechseck

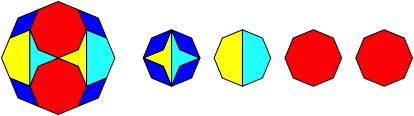
Abb. 1.8: Achteck

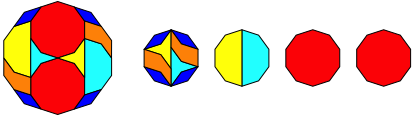
Abb. 1.10: Zehneck

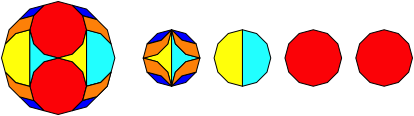
Abb. 1.12: Zwölfeck

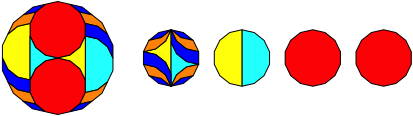
Abb. 1.14: Vierzehneck

2.2 Etwas eleganter

Abb. 2.4: Quadrat

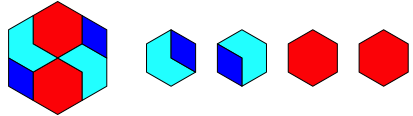
Abb. 2.6: Sechseck

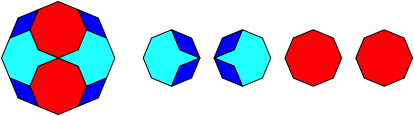
Abb. 2.8: Achteck

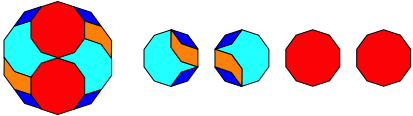
Abb. 2.10: Zehneck

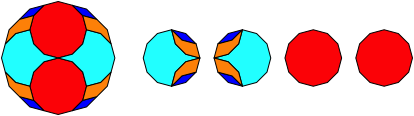
Abb. 2.12: Zwölfeck

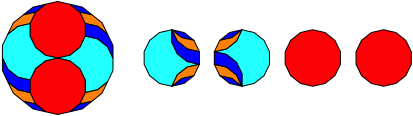
Abb. 2.14: Vierzehneck

2.3 Drehsymmetrie

Bei durch vier teilbaren Eckenzahlen gibt es Lösungen mit vierteiliger Drehsymmetrie.

Abb. 3.4: Quadrat

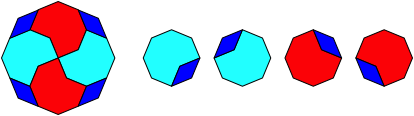
Abb. 3.8: Achteck

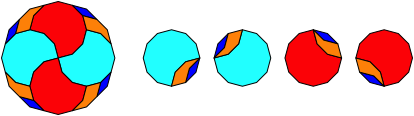
Abb.3.12: Zwölfeck

2.4 Mit Rhomben

Abb.4.4: Quadrat

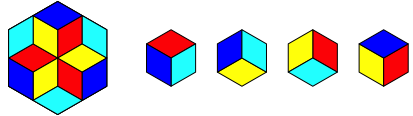
Abb. 4.6: Sechseck

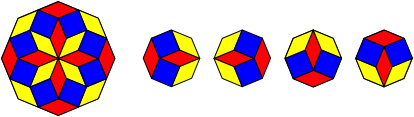
Abb. 4.8: Achteck

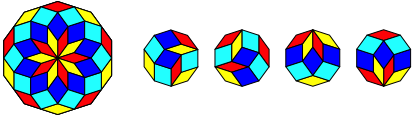
Abb. 4.10: Zehneck

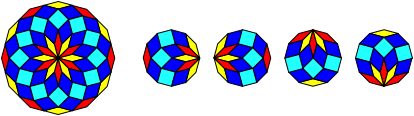
Abb. 4.12: Zwölfeck

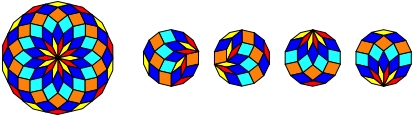
Abb. 4.14: Vierzehneck

Websites

Hans Walser: Vierteln regelmäßiger Vielecke

http://www.walser-h-m.ch/hans/Miniaturen/V/Vierteln/Vierteln.htm

Literatur

Frederickson, Greg N. (1997): Dissections: plane & fancy. Cambridge University Press.

Frederickson, Greg N. (2002): Hinged Dissections. Swinging & Twisting. Cambridge University Press. ISBN 0-521-81192-9. http://www.cs.purdue.edu/homes/gnf/book2.html

Hadwiger, Hugo (1949/50): Zum Problem der Zerlegungsgleichheit der Polyeder. Archiv der Math. 2, 441-444.

Hadwiger, Hugo (1954): Zum Problem der Zerlegungsgleichheit k-dimensionaler Polyeder. Math. Annalen, Bd. 127, 170-174.

Lindgren, Harry (1972): Geometric Dissections. Revised and enlarged by Greg Frederickson. New York: Dover.

Walser, Hans (1983): Ein Zerlegungssatz für punktsymmetrische konvexe Vielecke. Elemente der Mathematik (38), 1983, p. 159-160.