Hans Walser, [20071124a]
Die vivianische Kurve in stereographischer Projektion – die Strophoide
Anregung: [Kroll 2007]
1 Die vivianische Kurve
Die
vivianische Kurve kann durch 
beschrieben
werden.
Die vivianische Kurve
Von oben sieht das so aus:
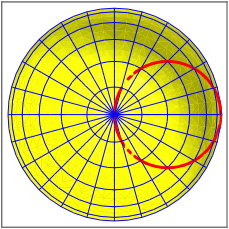
Sicht von oben
Die vivianische Kurve erscheint als Kreis. TatsŠchlich kann die vivianische Kurve auch als Schnittfigur der Einheitskugel mit einem stehenden Zylinder durch Kugelmittelpunkt und einen Punkt auf dem €quator beschrieben werden.
Von der Seite sieht das so aus:
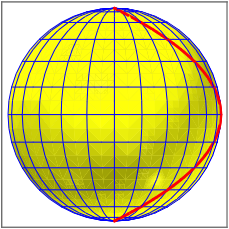
Sicht von der Seite
Die vivianische Kurve erscheint als liegende Standardparabel. Die vivianische Kurve kann also auch als Schnittfigur der Einheitskugel mit einem liegenden Zylinder mit parabolischem Profil beschrieben werden.
2 Stereografische Projektion
Fźr die stereographische Projektion (Zentralprojektion vom Nordpol auf die €quatorebene) arbeiten wir mit den Abbildungsgleichungen:
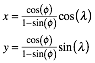
Wir erhalten die folgende Kurve, welche als Strophoide bezeichnet wird.
Link: http://de.wikipedia.org/wiki/Strophoide
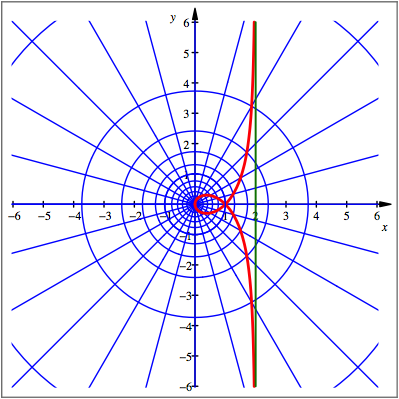
Die vivianische Kurve in stereografischer Projektion – die Strophoide
3 Die Asymptote
Interessant
ist die Asymptote der Strophoide bei 
. Dies kann auf zwei Arten eingesehen werden.
3.1 Einsicht durch Rechnen
Fźr die
vivianische Kurve gilt 
, somit bis auf Vorzeichen:
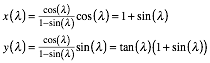
Daraus ergibt sich:
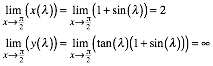
3.2 Einsicht durch Geometrie
Wir
bringen den Krźmmungskreis der vivianischen Kurve im Nordpol ins Spiel. Dieser
liegt auf der Kugel, da diese trivialerweise die Schmiegungskugel der
vivianischen Kurve ist. Die Schmiegungsebene der vivianischen Kurve im Nordpol
erscheint aus Symmetriegrźnden in der Sicht von der Seite als Tangente an die
liegende Standardparabel und schneidet die x-Achse
bei 
. Der Krźmmungskreis als Schnittkreis der Schmiegungskugel
mit der Schmiegungsebene ist also ein Kleinkreis durch den Nordpol und
erscheint in der stereografischen Projektion als Gerade 
.
Das stereografische Bild des Krźmmungskreises im Sźdpol entsteht durch Kreisspiegelung dieser Geraden am Hauptkreis (Bild des €quators, Einheitskreis).
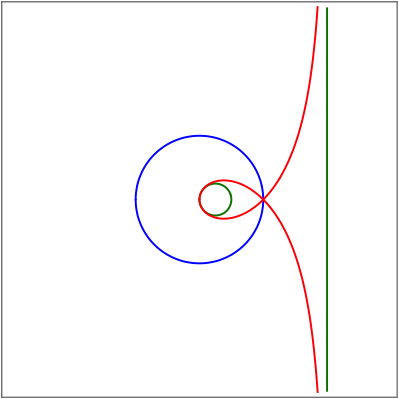
Kurve, Hauptkreis und Krźmmungskreise in den Polen
4 Planimetrische Konstruktion
Die Strophoide kann rein planimetrisch erzeugt werden:
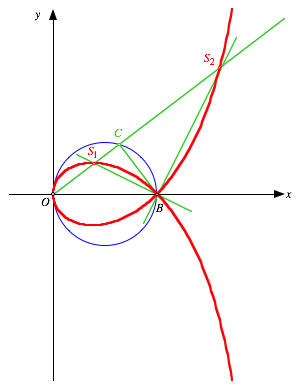
Planimetrisches Vorgehen
Auf dem
Thaleskreis źber 
wŠhlen wir einen
Punkt 
und schneiden im
Dreieck 
die innere und
Šu§ere Winkelhalbierende des Winkels bei B
mit der Gegenseite von B. Die beiden
Schnittpunkte liegen auf der Strophoiden.
Der
Beweis sei dem Leser źberlassen. Tipp: der Dreieckswinkel bei O ist 
.
Literatur:
[Kroll 2007] Kroll,
Wolfgang: RŠumliche Kurven und FlŠchen in phŠnomenologischer Behandlung. © 2007
by Wolfgang Kroll, Marburg. ISBN 978-3-00-021836-1
http://www.sciface.com/education/data/more/krollkuf/index.html