Hans Walser, [20160611]

Viviani-Flächensatz

1 Worum geht es?

Es wird ein Flächensatz im gleichseitigen Dreieck besprochen.

Der Längen-Satz von Viviani besagt, dass in einem gleichseitigen Dreieck die Summe der drei Lotstrecken h_a, h_b, h_c von einem beliebigen Punkt P zu den Dreieckseiten (Abb. 1) eine Konstante ist, nämlich die Dreieckshöhe h (Vargyas und Walser, 2015).

(1)

Für P außerhalb des Dreieckes muss mit Vorzeichen (orientierter Abstand) gearbeitet werden.

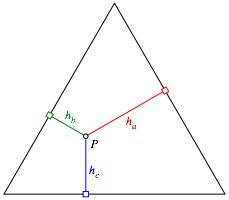
Abb. 1: Der Längen-Satz von Viviani

Wir ergänzen nun die Figur durch drei kleine gleichseitige Dreiecke (Abb. 2). Sie haben einen gemeinsamen Eckpunkt in P und je eine Seite auf je einer der drei Dreiecksseiten des Ausgangsdreieckes.

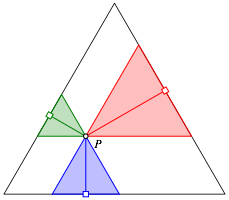
Abb. 2: Kleine gleichseitige Dreiecke

Die Summe der drei kleinen Dreiecksflächen ist keine Konstante. Für P im Mittelpunkt des Ausgangsdreieckes ist der Flächensummenanteil am ganzen Dreieck ein Drittel. Für P als Mittelpunkt einer Dreiecksseite ergibt sich ein Flächensummenanteil von einem Halben. Eines der drei kleinen Dreiecke verschwindet. Für P in einer Dreiecksecke verschwinden sogar zwei der drei kleinen Dreiecke, das dritte wird deckungsgleich zum Ausgangsdreieck. Der Flächensummenanteil ist eins.

Wir fragen nach den Bedingungen für P, um einen konstanten Flächensummenanteil zu erhalten. Das Vorgehen ist rechnerisch.

2 Berechnung des Flächensummenanteils

Wir verwenden Disposition und Bezeichnungen gemäß Abbildung 3.

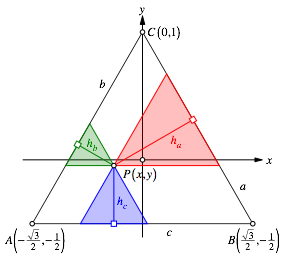
Abb. 3: Bezeichnungen

Das Dreieck ABC hat die Seitenlänge und die Höhe . Sein Flächeninhalt ist .

Für die Seitengeraden a, b, c des Dreieckes ABC erhalten wir die Hesseschen Normalformen:

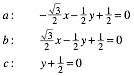(2)

Somit ist:

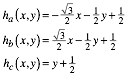(3)

Durch Addition folgt unmittelbar , also (1).

Für den Flächensummenanteil f(x,y) der drei kleinen Dreiecke im Verhältnis zum Ausgangsdreieck ergibt sich mit etwas Rechnung:

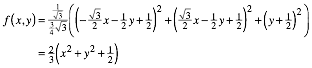(4)

3 Konstanter Flächensummenanteil

Für einen konstanten Flächensummenanteil ist (4) eine Kreisgleichung.

Die Abbildung 4 zeigt die Niveaulinien von für die Anteile (Mittelpunkt des Dreieckes), , (Inkreis des Dreieckes), , , , , , (Umkreis des Dreieckes).

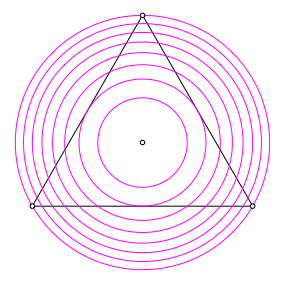
Abb. 4: Niveaulinien

4 Beispiele mit Inkreis

4.1 Halber Flächenanteil

Für einen Punkt P auf dem Inkreis (Abb. 5) ist der Flächensummenanteil die Hälfte.

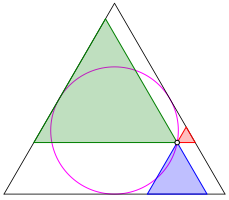
Abb. 5: Halber Anteil

4.2 Ganzzahlige Lösungen im Dreiecksraster

Die Abbildungen 6 und 7 zeigen ganzzahlige Lösungen im Dreiecksraster mit je einem „Neunpunkte-Inkreis“.

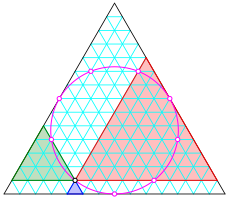
Abb. 6: Ganzzahlige Lösung

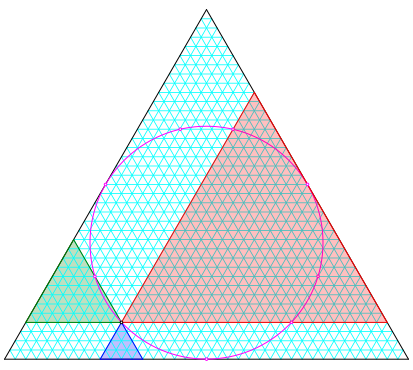
Abb. 7: Ganzzahlige Lösung

Ganzzahlige Lösungen im Dreiecksraster finden wir mit brute force wie folgt. Mit x, y, z bezeichnen wir die Seitenlängen der drei kleinen Dreiecke. Für die Seitenlänge s des Ausgangsdreiecks gilt dann:

(5)

Die Flächenbedingung (halber Flächenanteil) führt auf:

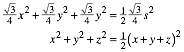(6)

Wir normieren die Reihenfolge auf und beschränken uns auf teilerfremde Zahlen x, y, z. Die Tabelle 1 gibt die ersten Lösungen.

x + y + z	x	y	z	Bem.
6	4	1	1
14	9	4	1	Abb. 6
26	16	9	1
38	25	9	4	Abb. 7
42	25	16	1
62	36	25	1
74	49	16	9
78	49	25	4
86	49	36	1
98	64	25	9
114	64	49	1
122	81	25	16
134	81	49	4
146	81	64	1
158	100	49	9
182	100	81	1

Tab. 1: Ganzzahlige Lösungen

Literatur

Vargyas, Emese und Walser, Hans (2015): Verallgemeinerung des Satzes von Viviani. MI, Mathematikinformation Nr. 63, 15. September 2015. ISSN 1612-9156. S. 3-10.

Websites

Abgerufen 11.06.2016

Viviani im Raum:

www.walser-h-m.ch/hans/Miniaturen/V/Viviani_3d/Viviani_3d.htm

Viviani-Simplex:

www.walser-h-m.ch/hans/Miniaturen/V/Viviani_Simplex/Viviani_Simplex.htm