Hans Walser, [20130610], [20131020]
Voronoi-Regionen
1 Einzugsbereiche von Punkten
Einstiegsbeispiel: Angenommen, die schwarzen Punkte der Abbildung 1 seien Standorte von zum Beispiel Schulhusern oder Pumpstationen. Wie finden wir die optimalen Einzugsbereiche? Optimal hei§t hier, dass der Weg zu einem Punkt mglichst kurz sein soll. Also mglichst kurze Schulwege. Andere Einkleidung: Nchster Flughafen fr eine allfllige Landung in einer Notsituation. Oder: Einsatzbereich von Sttzpunktfeuerwehren.
Die Einzugskapazitt der Attraktor-Punkte wird als unlimitiert angenommen.
Die Einzugsbereiche finden wir mit Mittelsenkrechten.
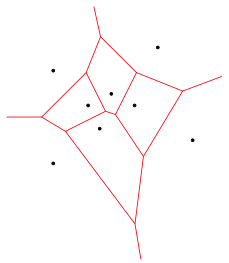
Abb. 1: Voronoi-Regionen
Die Einzugsbereiche werden als Voronoi-Regionen bezeichnet. Die schwarzen Punkte sind die Zentren der Voronoi-Regionen. Innerhalb einer Voronoi-Region ist ihr Zentrum der nchste der Punkte.
Das Netz der roten Mittelsenkrechten hei§t Voronoi-Diagramm. Andere Bezeichnungen sind Thiessen-Polygone oder Dirichlet-Zerlegung.
Die Knotenpunkte des Voronoi-Diagramms sind Mittelpunkte von Kreisen, welche durch Zentren von Voronoi-Regionen laufen.
Die duale Figur zum Voronoi-Diagramm wird als Delone-Triangulation bezeichnet (Abb. 2). Die Voronoi-Regionen zweier in der Delone-Triangulation miteinander verbundener Punkte haben eine Grenze gemeinsam, sind also benachbart.
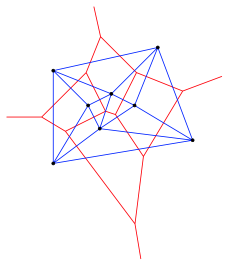
Abb. 2: Delone-Triangulation
Die Abbildung 3 zeigt eine andere Triangulation. Die grn eingezeichneten Strecken verbinden jeweils zwei Punkte, deren Voronoi-Regionen nicht benachbart sind. Gefhlsm§ig: die grnen Strecken sind ãzu langÒ. Die Triangulation ist nicht optimal.
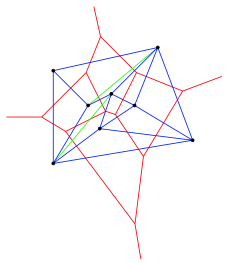
Abb.3: Andere Triangulation
2 Einzugsbereiche von Inseln
Vorstellung: In einem Archipel befinden sich mehrere Inseln. Der Voronoi-Bereich einer Insel ist derjenige Bereich (im Meer), von dessen Punkten aus die Strecke zur Insel am krzesten ist. Minimale Schwimmstrecke fr Schiffbrchige.
Es werden einige nicht realistische Flle untersucht. Sie knnen mit DGS (GeoGebra) gezeichnet werden.
2.1 Zwei kreisfrmige Inseln
Anstelle der Mittelsenkrechten ergibt sich eine Hyperbel als Grenzlinie (Abb. 4).
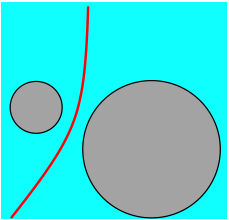
Abb. 4: Zwei Inseln
2.2 Drei Inseln
Drei Hyperbelbgen.
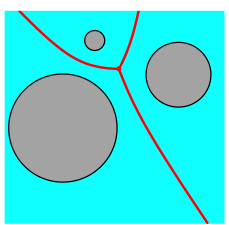
Abb. 5: Drei Inseln
2.3 Drei Inseln und Festland
Drei Hyperbelbgen und zwei Parabelbgen.
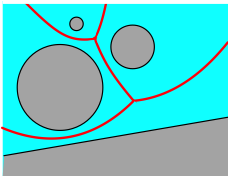
Abb. 6: Drei Inseln und Festland
2.4 Die Insel im Ententeich
Die Grenzlinie ist eine Ellipse.

Abb. 7: Insel im Ententeich
2.5 Zwei Inseln
Ellipsenbgen und ein Hyperbelbogen

Abb. 8: Zwei Inseln im Ententeich
2.6 Runde Insel im quadratischen Ententeich
Parabelbgen

Abb. 9: Runde Insel im quadratischen Ententeich
2.7 Quadratische Insel
Mittelparallelen und Parabelbgen

Abb. 10: Quadratische Insel im quadratischen Ententeich