1 Worum es geht

Spielerei im Umfeld des Satzes von van Aubel.

Auflistung von Resultaten.

2 Startviereck

Wir beginnen mit einem beliebigen Viereck (gelb in Abb. 1) und seinem Eckenschwerpunkt.

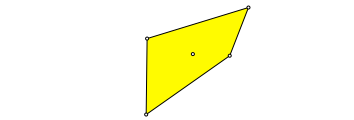
Abb. 1: Startviereck

3 Quadrate ansetzen

Jeder Viereckseite setzen wir ein Quadrat mit seinem Mittelpunkt an (blau in Abb. 2).

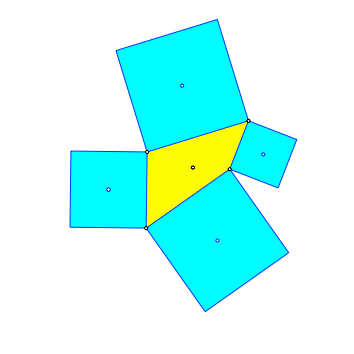
Abb. 2: Quadrate ansetzen

Die vier Quadratmittelpunkte haben den Eckenschwerpunkt des gelben Startviereckes als Schwerpunkt.

4 Der Satz von van Aubel

Die Verbindungsstrecken gegenüberliegender Quadratmitten (blau in Abb. 3) sind orthogonal und gleich lang. Dies ist der Satz von van Aubel.

Abb. 3: Orthogonale und gleich lange Strecken

5 Thaleskreise

Wir machen die Orthogonalität mit Thaleskreisen sichtbar (rot in Abb. 4).

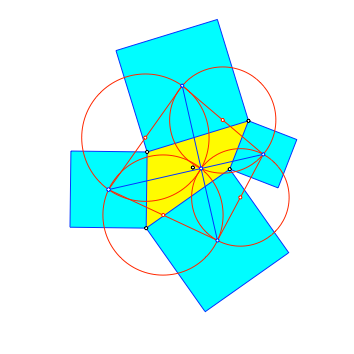
Abb. 4: Thaleskreise

Die Mittelpunkte der vier Thaleskreise sind die Ecken eines Quadrates (rot in Abb. 5). Das rote Quadrat ist parallel zu den blauen Verbindungsstrecken, die Quadratseiten sind halb so lang. Dies folgt aus dem Satz von van Aubel mit Strahlensätzen.

Der Mittelunkt des roten Quadrates ist der Eckenschwerpunkt des gelben Startvierecks.

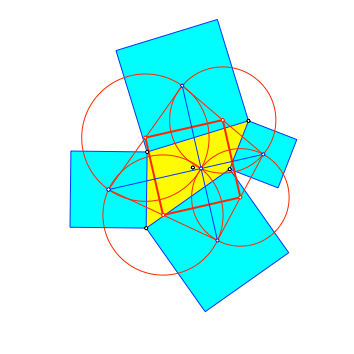
Abb. 5: Noch ein Quadrat

6 Schnittpunkte

Die vier roten Thaleskreise schneiden sich wegen der Orthogonalität der blauen Verbindungsstrecken im Schnittpunkt dieser Verbindungsstrecken.

Je zwei gegenüberliegende Thaleskreise haben aber noch einen Schnittpunkt. Jeder dieser beiden Schnittpunkte liegt auf einer Diagonalen des gelben Startviereckes (Abb. 6). Die Schnittpunkte sind also „besondere Punkte“.

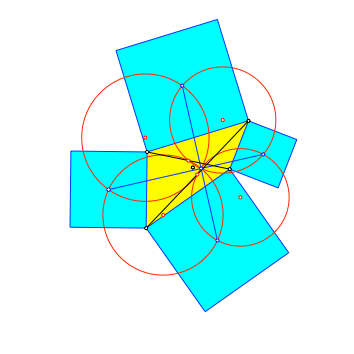
Abb. 6: Zwei Schnittpunkte

Der Eckenschwerpunkt des gelben Startviereckes ist der Mittelpunkt dieser beiden besonderen Schnittpunkte.

7 Iteration

Nun zeichnen wir die Quadrate über den Endpunkten der blauen Verbindungsstrecken (grün in Abb. 7). Die Quadratmittelpunkte liegen auf den Thaleskreisen.

Der Schwerpunkt der Quadratmittelpunkte ist wiederum der Eckenschwerpunkt des gelben Startviereckes.

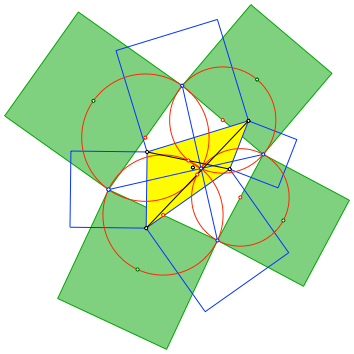
Abb. 7: Nochmals vier Quadrate

Die alternierende Flächensumme der vier grünen Quadrate ist null. Dies kann mit dem Satz von Pythagoras gezeigt werden.

Wir können nun wiederum den Satz von van Aubel ins Spiel bringen (Abb. 8).

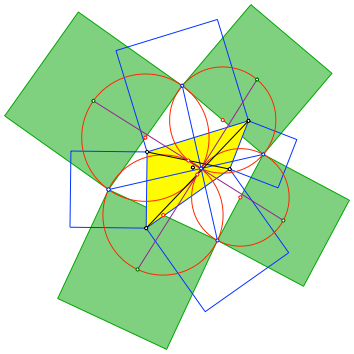
Abb. 8: Lila Verbindungsstrecken

Die lila Verbindungsstrecken der Mittelpunkte der grünen Quadrate verlaufen durch den Schnittpunkt der blauen Verbindungsstrecken und schneiden diese unter Winkeln von 45°. Die Länge der lila Verbindungsstrecken ist das √2-fache der Länge der blauen Verbindungsstrecken. Wir sind offenbar daran, das Quadrat neu zu erfinden.

Die lila Verbindungsstrecken verlaufen weiter durch die Schnittpunkte der Thaleskreise mit den Diagonalen des gelben Startviereckes. Das sind nun also ganz besondere Punkte.