Hans Walser, [20100331a], [20160710]

Van Schooten’s Theorem

Anregung: Chr. P., B.

1 Worum geht es?

Im gleichseitigen Dreieck gilt ein eigenartiger Summensatz (van Schooten’s Theorem), der sich als Sonderfall des Satzes von Ptolemäus erweist.

Das van Schooten’s Theorem wird verallgemeinert.

2 Gleichseitiges Dreieck

Auf dem Bogen AB des Umkreises eines gleichseitigen Dreieckes ABC wählen wir einen Punkt P (Abb. 1). Die Sehnen PA, PB und PC bezeichnen wir mit x, y, z. Dann gilt van Schooten’s Theorem:

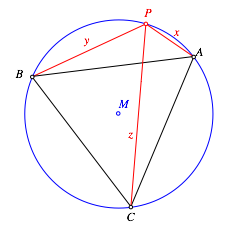
Abb. 1:

Frans van Schooten (1615-1660), niederländischer Mathematiker.

3 Beweise

(Viglione 2016) gibt einen schönen Beweis ohne Worte.

3.1 Beweis mit einer Drehung

Die Peripheriewinkel und messen beide 60°, da die zugehörigen Zentriwinkel je 120° messen.

Wir drehen nun das gelbe Dreieck APB um A um 60° (Abb. 2). Das Bilddreieck ist AQC mit . Das Dreieck APQ ist gleichseitig.

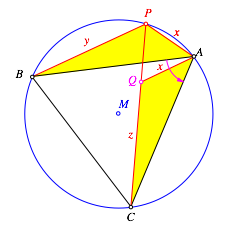
Abb. 2: Beweisfigur

Somit ist .

3.2 Beweis mit dem Satz des Ptolemäus

Das Viereck APBC ist ein Sehnenviereck. In einem Sehnenviereck ist nach dem Satz des Ptolemäus das Produkt der Diagonalen gleich der Summe der Produkte von je zwei gegenüberliegenden Seiten.

Mit der Seitenlänge s des gleichseitigen Dreiecks heißt das in unserem Fall:

Daraus folgt unmittelbar van Schooten’s Theorem.

3.3 Beweis mit dem Kosinus-Satz

Es sei s die Seitenlänge des gleichseitigen Dreieckes ABC und r dessen Umkreisradius. Wir machen nun eine Fallunterscheidung:

(i) . Der Punkt P liegt in der Mitte des Bogens AB. Es ist und , somit .

(ii) . Im Dreieck APC liefert der Kosinus-Satz:

Im Dreieck CPB erhalten wir analog:

Differenz der beiden Gleichungen:

4 Verallgemeinerungen

4.1 Quadrat

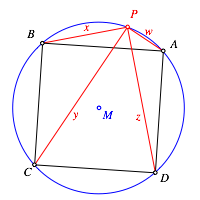
Abb. 3: Quadrat

In der Situation der Abbildung 3 gilt:

Beweis:

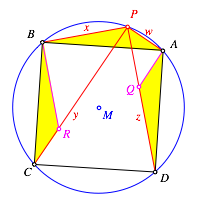
Abb. 4: Beweisfigur

Durch Drehen des Dreiecks APB um A um 90° beziehungsweise um B um –90° folgt:

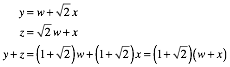
4.2 Pentagon

Es versteht sich von selbst, dass hier der goldene Schnitt erscheinen muss (Walser 2001), (Walser 2013). Wir verwenden die Schreibweise:

Die Abbildung 5 zeigt die Situation im Pentagon.

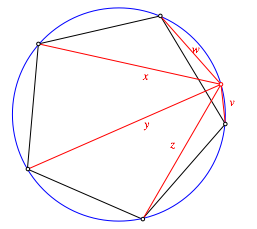
Abb. 5: Pentagon

Mit den Bezeichnungen der Abbildung 5 gilt:

Für den Beweis der ersten Zeile verwenden wir die beiden in der Abbildung 6 angedeuteten Drehungen um 108° beziehungsweise –108°.

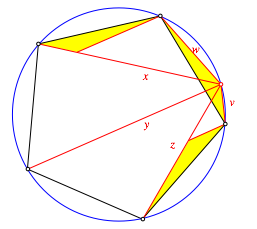
Abb. 6: Beweisfigur mit zwei Drehungen

Es ist dann:

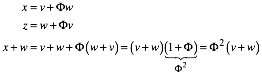
Für den Beweis der zweiten Zeile verwenden wir die in er Abbildung 7 angedeutete Drehstreckung mit dem Drehwinkel 72° und dem Streckfaktor .

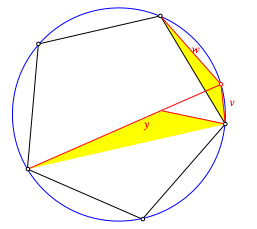
Abb. 7: Beweisfigur mit einer Drehstreckung

Es ist:

Insgesamt haben wir:

Die weitere Verallgemeinerung auf das reguläre n-Eck sei der geneigten Leserin überlassen.

5 Allgemeines Dreieck

Bezeichnungen gemäß Abbildung 8.

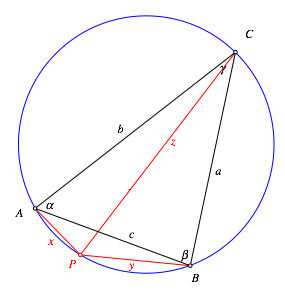
Abb. 8: Allgemeines Dreieck

Es gilt:

Bemerkung: Das ist der Satz des Ptolemäus.

Der Satz des Ptolemäus wird in der Regel so formuliert, dass in einem Sehnenviereck (bei uns das Viereck APBC) das Produkt der beiden Diagonalen (bei uns cz) gleich ist der Summe der Produkte von je zwei gegenüberliegenden Seiten (bei uns ).

Für den Beweis arbeiten wir mit den Bezeichnungen der Abbildung 9.

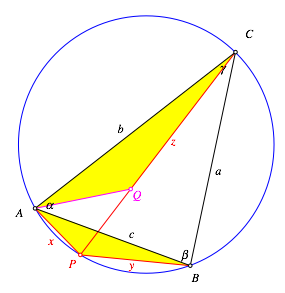
Abb. 9: Beweisfigur

Wir bilden das Dreieck APB mit einer Drehstreckung auf das Dreieck AQC ab. Drehzentrum A, Drehwinkel , Streckfaktor . Mit Winkelüberlegungen kann gezeigt werden, dass das Dreieck APQ ähnlich ist zum Dreieck ABC und dass .

Somit ist:

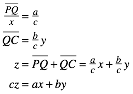
Literatur

Viglione, Raimund (2016): Proof Without Words: van Schooten’s Theorem. Mathematics Magazine 89 (2016) 132.

Walser, Hans (2001): The Golden Section. Translated by Peter Hilton and Jean Pedersen. The Mathematical Association of America 2001. ISBN 0-88385-534-8.

Walser, Hans (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wußing über populärwissenschaftliche Mathematikliteratur aus Leipzig. Edition am Gutenbergplatz, Leipzig. ISBN 978-3-937219-85-1.