Hans Walser, [20160429]

Winkelaufgabe

1 Die Aufgabe

Eine klassische Aufgabe besteht darin, in der Figur der Abbildung 1 den angegebenen Winkel zu bestimmen. Es wird eine bildorientierte Lösung vorgestellt.

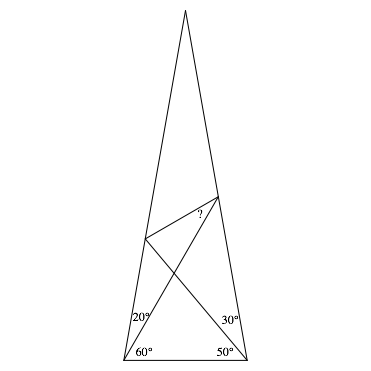
Abb. 1: Wie groß ist der gesuchte Winkel?

Einige eigene Lösungsversuche sind ratsam, um den Schwierigkeitsgrad der Aufgabe zu erleben.

Natürlich kann man das Problem zeichnerisch angehen. Der gesuchte Winkel misst 30°. Aber wie lässt sich das beweisen?

2 Stern mit neun Spitzen

Nach Einzeichnen eines gleichseitigen Dreieckes (rot in Abbildung 2) sehen wir, dass wir die Figur in einen Stern mit neun Spitzen einpassen können. Der Schlüssel dazu ist das gleichschenklige Dreieck (verfärbtes Blau) mit dem Spitzenwinkel 80° und den Basiswinkeln 50°.

Abb. 2: Stern mit neun Spitzen

Hier zeigt sich auch, dass sich die Sache nicht mit Zirkel und Lineal angehen lässt, da ein regelmäßiges Neuneck nicht mit Zirkel und Lineal konstruierbar ist.

3 Ein Rechteck

Mit Hilfe zweier Rhomben (magenta in Abbildung 3) und eines gleichseitigen Dreiecks (grün) sowie einer Symmetrieüberlegung zeigen wir, dass das braune Viereck ein Rechteck ist.

Abb. 3: Rechteck

4 Rechtwinkliges Dreieck

Daraus folgt nun aber, dass das lila Dreieck in der Abbildung 4 rechtwinklig ist. Der eine der beiden spitzen Winkel misst 60°. Daher muss der andere spitze Winkel 30° messen. Das ist aber unser gesuchter Winkel.

Abb. 4: Rechtwinkliges Dreieck

5 Isoliertes Beispiel

Wir konnten unsere Aufgabe mit einem Neuneck und einem zugehörigen Stern lösen. Das lag an den gegebenen Daten und ist leider nicht verallgemeinerungsfähig.

Wer’s nicht glaubt, versuche das leicht modifizierte Problem der Abbildung 5 zu lösen.

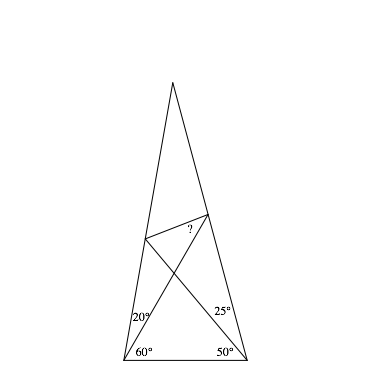
Abb. 5: Modifiziertes Problem

Das Resultat ist (Dynamische Geometrie Software) etwa 38.73789306893789°.