Hans Walser, [20090304a], [20131023]

Winkeldefizite bei konvexen Polyedern

Anregungen: [Heinrich 2009], J. P. und P. H.

1 Worum es geht

Die Summe der ebenen Winkel in einer konvexen Polyederecke ist kleiner als 360°. Zu jeder Polyederecke gibt es also ein Winkeldefizit als Ergänzung auf 360°.

Die Summe dieser Winkeldefizite ist konstant, nämlich 720°. Die Gedankengänge gehen auf René Descartes (1596-1650) zurück.

René Descartes (1596-1650). (Zeichnung B. S.)

Die Formel von Descartes ist äquivalent zur Polyederformel von Euler (1707-1783).

2 Das Winkeldefizit

Die Summe der ebenen Winkel in einer konvexen Polyederecke (das heißt die Summe der Winkel, die zwischen den Kanten eine konvexen Ecke entstehen) ist kleiner als 360°.

2.1 Beispiele

Wir bezeichnen mit E die Anzahl der Ecken, mit K die Anzahl der Kanten und mit F die Anzahl der Seitenflächen eines Polyeders.

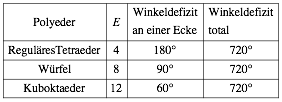
Das totale Winkeldefizit scheint eine Invariante zu sein.

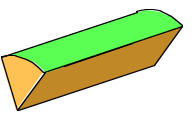
Ein weniger regelmäßiges Beispiel: Wir setzen einem Würfel eine Pyramide auf, deren Seitenflächen gleichschenklige Dreieck mit 36° an der Spitze sind.

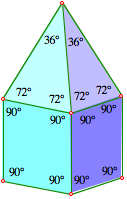
Würfel mit Pyramidendach

Das Polyeder hat vier Basisecken mit einem Winkeldefizit von je 90°, vier Ecken an der Pyramidenbasis mit einem Winkeldefizit von je 36°° und die Spitze mit einem Winkeldefizit von 216°. Das totale Winkeldefizit ist .

3 Der Satz von Descartes

Das totale Winkeldefizit eines konvexen Polyeders ist .

3.1 Beweis mit sphärischem Bild

Wir denken uns zum Polyeder die äußere „Parallelfläche“ im Abstand 1. Das ist die Menge aller Punkte, welche im Außenraum des Polyeders liegen und von der Oberfläche des Polyeders den Abstand 1 haben. Die Abbildung zeigt links den Würfel und rechts seine Parallelfläche.

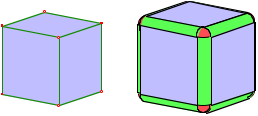
Würfel und Parallelfläche

Die folgende Abbildung zeigt allgemein eine Polyederecke und ihre Parallelfläche.

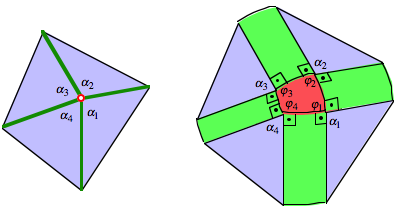
Polyederecke und Parallelfläche

Die Parallelfläche besteht zunächst aus ebenen Flächenstücken, welche zu den ursprünglichen Seitenflächen kongruent sind. Den ursprünglichen Seitenflächen sind gerade Prismen der Höhe 1 aufgesetzt.

Über den ursprünglichen Kanten liegen Zylindersektoren. Solche Zylindersektoren kann man sich als Spälten (Spaltholz) denken, welche beim Scheiten (Holzhacken) aus Trämeln (Rundholz) entstehen.

Zylindersektor

Die ursprünglichen Kanten des Polyeders sind die Zylinderachsen, die Sektorwinkel sind die Außenwinkel des jeweiligen Winkels zwischen den Flächen an der betreffenden Kante. Die Abwicklungen der Mantelflächen dieser Zylindersektoren sind Rechtecke.

Über den ursprünglichen Ecken ergeben sich sphärische Vielecke. Die Abbildung zeigt ein sphärisches Viereck.

Sphärisches Vieleck

Die Innenwinkel dieser sphärischen Vierecke sind die Ergänzungswinkel der anstoßenden Seitenflächenwinkel auf , da wir im selben Punkt noch zwei rechte Winkel von den Zylindersektoren haben. Ein solches sphärisches Vieleck wird als sphärisches Bild der betreffenden Polyederecke bezeichnet. Je „spitzer“ die Ecke, um so größer das sphärische Bild.

Für den Flächeninhalt dieser sphärischen Vielecke verwenden wir die Formel:

Dabei sind die Innenwinkel des sphärischen Vieleckes und n die Eckenzahl. Ist der anstoßende Winkel der ebenen Seitenfläche, so ist . Für den Flächeninhalt des sphärischen Vieleckes erhalten wir:

Das ist aber das Winkeldefizit an der betreffenden Ecke.

Nun können wir — und das ist das entscheidende Argument in der Beweisführung —

die sphärischen Vielecke aller Ecken passgenau zur Einheitskugel zusammenfügen.

Diese hat den die Gesamtoberfläche . Somit ist das totale Winkeldefizit .

3.2 Äquivalenz zur Polyederformel von Euler

An jeder Polyederecke ist das Winkeldefizit minus die Summe der anstoßenden Seitenflächenwinkel. Das totale Winkeldefizit ist somit minus die totale Summe aller Seitenflächenwinkel. Diese totale Winkelsumme berechnen wir nun über die Seitenflächen. Für eine Seitenfläche erhalten wir die Winkelsumme als , wobei n die Eckenzahl und damit auch die Kantenzahl dieser Seitenfläche ist. Da zu jeder Kante genau zwei Seitenflächen gehören, ist die totale Winkelsumme gleich . Für das totale Winkeldefizit erhalten wir somit

Daher ist:

Die Aussage wird als Eulersche Polyederformel bezeichnet.

Leonhard Euler (1707-1783). (Zeichnung B. S.)

3.3 Analogie zur Außenwinkelsumme bei ebenen Polygonen

Zu einem ebenen konvexen Polygon zeichnen wir die äußere „Parallelkurve“ im Abstand 1. Diese besteht aus Strecken, welche kongruent zu den Polygonkanten sind sowie Kreissektoren über den Ecken. Die Sektorenwinkel sind die Außenwinkel des Polygons. Diese Sektoren können wir passgenau zum Einheitskreis zusammensetzen. Daher ist die Außenwinkelsumme gleich 2π.

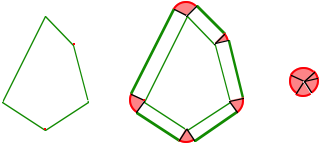
Polygon, Parallelkurve und Eckenbild

4 Anwendung: Eckenreguläre Polyeder

Ein konvexes Polyeder mit kongruenten Ecken heißt eckenreguläres Polyeder. In diesem Fall haben alle Ecken dasselbe Winkeldefizit, dieses muss also ein Teiler von sein. Wir haben damit eine notwendige Bedingung, mit der wir rein rechnerisch gewisse Fälle ausschließen können.

Im Folgenden besprechen wir ausführlich ein konkretes Beispiel.

5 Ein Quadrat und zwei Dreiecke

5.1 Problemstellung

Beispiel nach [Heinrich 2009, S. 56]: An jeder Ecke sollen ein Quadrat und zwei reguläre Dreiecke zusammenstoßen. Das Winkeldefizit ist . Das ist kein Teiler von 720°. So geht es also nicht.

Natürlich kann das auch rein raumgeometrisch eingesehen werden: Wir beginnen gemäß Figur links mit einem roten Quadrat ABCD, einem grünen Dreieck BCE und einem blauen Dreieck CDE und bilden damit eine räumliche Ecke C. Nun sollten wir an der Ecke E ein Quadrat ansetzen, da wir schon zwei Dreiecke haben. Wir müssen also die drei Punkte DEB zu einem Quadrat DEBF ergänzen. An und für sich geht das problemlos, nur schneidet dieses Quadrat das rote Quadrat ABCD. Das Problem ist also die Selbstdurchdringung.

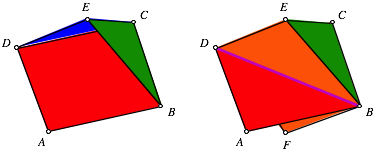
Selbstdurchdringung

5.2 Eckenfiguren

Wenn wir bei einem Polyeder eine Ecke abschneiden, erhalten wir als Schnittfigur die Eckenfigur der betreffenden Ecke. Tetraeder, Würfel und Dodekaeder haben regelmäßige Dreiecke als Eckenfiguren, das Oktaeder hat Quadrate als Eckenfiguren und das Ikosaeder regelmäßige Fünfecke. Die Ecke C in der obigen Figur, welche durch ein Quadrat und zwei Dreiecke gebildet wird, hat als Eckenfigur ein Dreieck, das man mit Vorteil als gleichschenklig rechtwinkliges Dreieck zeichnet.

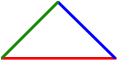
Eckenfigur der Ecke C

Die Eckenfigur ist ein Polygon, dessen Seiten den Seitenflächen des Polyeders und dessen Ecken den Kanten des Polyeders entsprechen.

5.3 Mehrfache Überlagerung

Nun machen wir aus der Not eine Tugend. Weil das Winkeldefizit von 150° nicht passt, machen wir es passend, indem wir das totale Winkeldefizit vergrößern. Das kleinste gemeinsame Vielfache des Winkeldefizits 150° und des totalen Winkeldefizits 720° ist:

Die Koeffizienten 24 und 5 in der obigen Gleichung haben beide, wie wir sehen werden, eine geometrische Bedeutung.

5.4 Oktaeder als Trägerfigur

Die Punkte A, B, C, D, E und F sind die Ecken eines regulären Oktaeders.

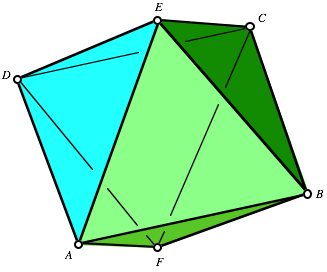
Oktaeder

Wir überlagern dieses Oktaeder mit einem neuen Polyeder: Das Oktaeder hat acht gleichseitige Dreiecke sowie im Innern drei Quadrate. Wir nehmen nun diese Flächenstücke je doppelt. Für das neue Polyeder gilt also:

Die 16 Dreiecke und 6 Quadrate haben insgesamt einzelne Ecken. Da an jeder Polyederecke zwei Dreiecke und ein Quadrat, also drei Seitenflächen zusammenstoßen, ergibt sich für das neue Polyeder:

Das neue Polyeder hat also 24 Ecken. Diese Zahl 24 kam schon oben bei der Berechnung des kleinsten gemeinsamen Vielfachen vor: . Damit das schön aufgeht, müssen wir also die 6 Ecken des Oktaeders je vierfach zählen.

Die 16 Dreiecke und 6 Quadrate haben insgesamt auch einzelne Kanten. Da an jeder Kante 2 Seitenflächen zusammenstoßen, ergibt sich für das neue Polyeder:

Das neue Polyeder hat also 36 Kanten. Wir müssen die 12 Kanten des Oktaeders je dreifach zählen.

Da wir jede Oktaederecke vierfach zählen, haben wir dort vier Eckenfiguren oder oben dargestellten Art. Die viere Eckenfiguren durchdringen sich gegenseitig.

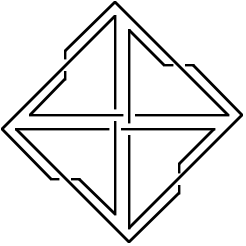
Eckenfiguren des neuen Polyeders, an einer Oktaederecke appliziert

Wir sehen, dass die Dreiecksseiten des Oktaeders je doppelt zu zählen sind („Randlinien“ der Figur) und ebenso die Quadrate im Innern („Diagonalen“ der Figur). Die Kanten des Oktaeders sind je dreifach zu zählen („Ecken“ der Figur).

Und wie steht es mit der Polyederformel von Euler? Wir erhalten:

Es ergibt sich das Fünffache des für ein gewöhnliches konvexes Polyeder geltenden Wertes 2. Diese Zahl 5 ist uns aber oben schon bei der Berechnung des kleinsten gemeinsamen Vielfaches begegnet: . Aber wie ist diese Zahl 5 geometrisch zu verstehen? Dazu studieren wir die Analogie zu ebenen Polygonen.

5.5 Analogie zu Polygonen

Für eine konvexes Polygon hatten wir die Außenwinkelsumme 360°. Bei einem eckenregulären Polygon muss also der Außenwinkel ein Teiler von 360° sein. Beispiel: Beim regulären Fünfeck haben wir einen Innenwinkel von 108° und somit einen Außenwinkel von 72°, einem Fünftel der Außenwinkelsumme von 360°. Wie ist es nun mit einem eckenregulären Polygon mit einem Innenwinkel von 36°? Wir haben in diesem Fall einen Außenwinkel von 144°, das ist aber kein Teiler von 360°. Für das kleinste gemeinsame Vielfache von 144° und 360° finden wir:

Das gesuchte Polygon hat also 5 Ecken. Eine mögliche Lösung ist das so genannte Pentagramm.

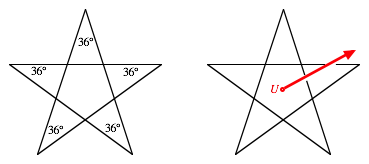
Pentagramm und ein Weg ins Freie

Ein Uruk-hai U, der sich aus dem Innern des Pentagramms ins Freie bewegen möchte, muss im Regelfall zwei Mal eine Polygonseite durchbrechen. Daher die Zahl zwei.

5.6 Zurück zu unserem Polyeder

Für einen Uruk-hai U im Zentrum unseres Polyeders ist es ein bisschen eng, weil dort drei Paare von wechselseitig orthogonalen Ebenen (die Quadrate, wir erinnern uns) durchlaufen. Der Uruk-hai sitzt also in einer infinitesimal kleinen kubischen Kiste, deren Wände aber außerhalb der Kiste weitergehen.

Ein Weg ins Freie muss daher im Regelfall drei der sechs Kistenwände durchbrechen. Im Beispiel der Figur ist die Seitenwand rechts bereits durchbrochen. Als nächstes müssen die Ebene der rückwärtigen Kistenwand und schließlich die Bodenebene durchbrochen werden.

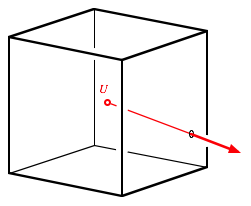
Der Weg aus der Kiste

Dann ist man aber noch nicht im Freien, sondern muss noch eine doppelt zu zählende Dreiecksfläche durchbrechen. Insgesamt also fünf Durchbrüche. Überzeugend, nicht?

5.7 Abwicklung

Und nun die Abwicklung unseres Polyeders. Doppelt zu zählende Flächen sind in der gleichen Farbe angegeben. Je die beiden Dreiecke gleicher Farbe erscheinen in dieser Abwicklung gleich orientiert. Je die beiden Quadrate gleicher Farbe erscheinen aber entgegengesetzt orientiert.

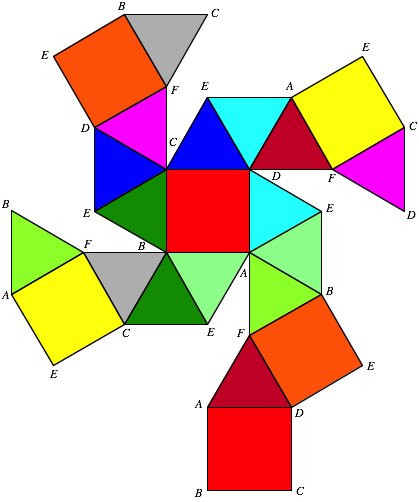
Abwicklung

Diese Abwicklung gibt Nachbarschaftsbeziehungen zwischen Flächenstücken wieder. Sie gestattet wegen der Selbstdurchdringungen aber nicht, das Polyeder als Modell zu bauen.

5.8 Modellbau

5.8.1 Bauteile

Die folgenden vier Bauteile für unser Polyeder nehmen auf die Selbstdurchdringungen Rücksicht. (Im Anhang sind die vier Bauteile vergrößert wiedergegeben.)

Bauteile

Da sich die Quadrate längs der Diagonalen gegenseitig durchdringen, enthalten die Bauteile immer nur Viertelquadrate. Wir haben insgesamt zum Beispiel acht rote Viertelquadrate, weil das rote Quadrat doppelt vorkommen muss. Die Dreiecke sind immer nur zu zwei Dritteln vorhanden. Es hat zum Beispiel drei dunkelblaue Zweidritteldreiecke, weil das dunkelblaue Dreieck doppelt vorkommen muss.

5.8.2 Bauvorgang

Die Bauteile sind auszuschneiden und längs der schwarzen Binnenkanten zu falten, sämtliche Faltlinien gehen in dieselbe Richtung. Die folgenden Fotos beziehen sich auf das Bauteil 1.

Ausschneiden und Falten

Im Zentrum des Bauteils erkennen wir je einen Viertel eines der drei Quadrate. Anschließend finden sich drei Zweitdritteldreiecke derselben Farbe. Wir fügen nun diese drei Zweidritteldreiecke zu einem doppelt überlagerten Dreieck zusammen. Auf der Außenseite sieht das dann aus gemäß der folgenden Foto.

Außenseite mit einem zusammengefügten Dreieck

Wir sehen, dass das Dreieck drei Durchdringungslinien hat, je von der Mitte aus zu einer Ecke. Dies kann man sich wie folgt erklären.

Wir sind alle so sozialisiert worden, dass bei der komplexen Funktion das Bild die w-Ebene doppelt überlagert wird, wie dies auch bei unserem Dreieck der Fall ist. Und das wird in der Regel so illustriert, dass längs eines vom Ursprung ausgehenden Strahls eine Durchdringungslinie zu denken ist.

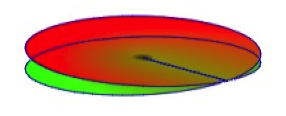
Riemannsche Fläche

Das ist aber willkürlich. Wir können eben so gut drei vom Ursprung ausgehende Durchdringungsstrahle nehmen.

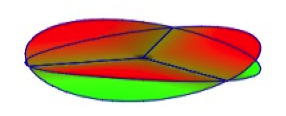
Variante: Drei Durchdringungslinien

Damit haben wir die Situation der Selbstdurchdringung unserer Dreiecke.

Auf der Innenseite unseres Modells entsteht eine Dreikantpyramide mit drei verschiedenfarbenen Viertelquadraten als Seitenflächen. Die Pyramidenspitze wird später zum Zentrum unseres Polyeders. Die Seitenflächen der Pyramide stellen einen Achtel der sich orthogonal durchdringenden Quadrate dar.

Innenseite

Wenn wir die äußersten Dreiecke, welche Viertelquadrate sind, einbiegen, erkennen wir, wie sich die drei sich gegenseitig orthogonal durchdringenden Quadrate weiterentwickeln.

Teile der drei Quadrate

Wir bearbeiten die drei übrigen Bauteile analog und fügen die Teile dann zusammen. Dabei können wir uns an den Farben orientieren. Im folgenden Bild sind drei der vier Teile zusammengefügt. Wir sehen immer noch in das Modell hinein. Insbesondere sehen wir schon fast die drei sich gegenseitig orthogonal durchdringenden Quadrate.

Drei der vier Teile sind zusammen

In der Schlussphase braucht es ein wenig sanfte Gewalt, Fingerspitzengefühl also.

Das fertige Modell ist von außen gesehen wenig spektakulär, ein Oktaeder eben.

Das fertige Modell

Literatur

[Heinrich 2009] Heinrich, Frank: Existenz- und Eindeutigkeitsbetrachtungen bei räumlichen archimedischen Gebilden. MU Der Mathematikunterricht. Polyeder im Mathematikunterricht. Jahrgang 55. Heft 1. Februar 2009. Friedrich Verlag, Seelze. S. 48-60

[Walser 2011] Hans Walser: Winkeldefizite bei konvexen Polyedern. Mathematikinformation, Nr. 54, 15. Januar 2011, S. 44-51. ISSN 1612-9156.

Anhang

Im Folgenden sind die vier Bauteile in Großformat wiedergegeben.

Tipp: Die vier Bauteile ausdrucken, die Figuren passgenau aufeinander legen und die vier Blätter außerhalb der Figuren mit Stapelklammern fixieren. Dann braucht man nur das oberste Bauteil mit Lineal und Japanmesser auszuschneiden. Den Schnitt möglichst auf der Innenseite der schwarzen Randlinie durchführen, damit wir beim Zusammenbau etwas Spielraum für die Papierdicke haben.

Bauteil 1

Bauteil 2

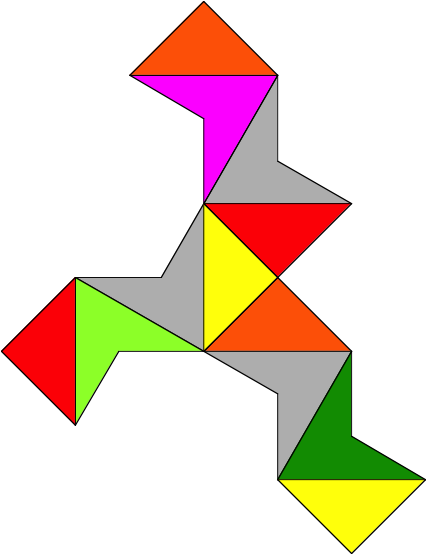
Bauteil 3

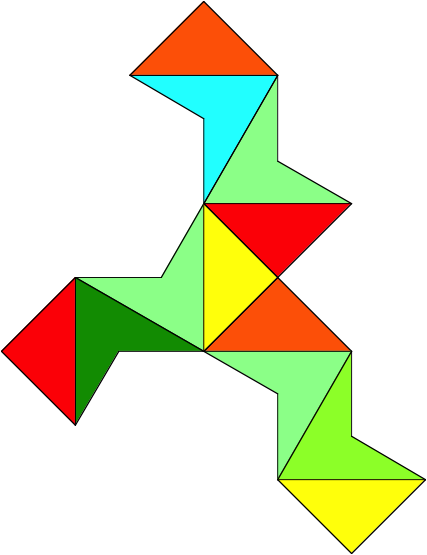
Bauteil 4