Hans Walser, [20080315a]
Winkeldrittelung
Anregung: Chr. W., B.
1 Worum es geht
Die Winkeldrittelung ist — zusammen mit der Wźrfelverdoppelung und der Quadratur des Kreises — eines der drei klassischen Probleme, die mit Zirkel und Lineal nicht lšsbar sind.
Hingegen lŠsst sich das Problem mit Schnittpunkten von Kegelschnitten angehen. Wir mźssen einen Kreis mit einer Hyperbel schneiden.
2 Disposition
Das Problem der Winkeldrittelung ist Šquivalent mit dem Problem, einen Kreisbogen in drei gleiche Teile zu teilen, oder dem Kreisbogen einen gleichseitigen Polygonzug mit drei Seiten einzubeschreiben.
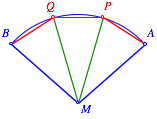
Winkeldrittelung
Wir
verwenden ein Koordinatensystem so, dass die Endpunkte A und B die Koordinaten 
beziehungsweise 
haben.
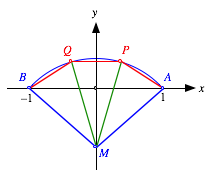
Disposition
3 Die Hyperbel
In diesem
Koordinatensystem ist der Punkt P von
der y-Achse halb so weit entfernt wie
vom Punkt A. Fźr seine Koordinaten 
gilt daher:
Durch
Quadrieren erhalten wir 
, also:
Dies ist die Gleichung einer Hyperbel. Der Drittelspunkt P ist also der Schnittpunkt des Winkelbogens AB mit dieser Hyperbel.
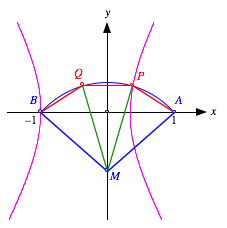
Schnitt mit Hyperbel
Interessant ist dabei, dass der zweite Hyperbelast nicht, wie ich zuerst erwartet habe, durch den zweiten Drittelspunkt Q verlŠuft, sondern durch den Endpunkt B des Winkelbogens. Zur Konstruktion des Punktes Q mźssen wir den Punkt P an der y-Achse spiegeln.
Die
Hyperbelgleichung 
lŠsst sich
umformen in die Standardform:
Die
Hyperbel hat also den Mittelpunkt 
, und mit den bei Kegelschnitten źblichen Bezeichnungen ist 
und 
. Die Brennpunkte sind 
und 
. Die beiden Asymptoten haben die Gleichungen
.
Mittelpunkt
und Radius des Kreisbogens sind fźr die Hyperbel irrelevant; der rechte
Hyperbelast und sein Spiegelbild dritteln jeden Kreisbogen mit den Endpunkten A und B. Insbesondere wird auch die Strecke 
gedrittelt.
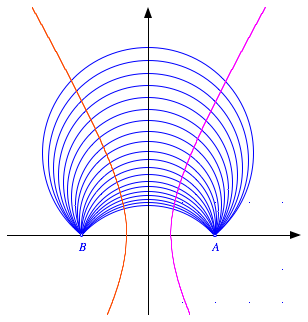
Jeder Kreisbogen wird gedrittelt
4 Der zweite Hyperbelast
Und wozu ist der zweite Hyperbelast gut? Das sehen wir im folgenden Bild:
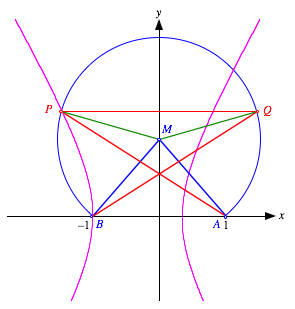
ă†berschlagenerŇ Polygonzug
Der gleichseitige Polygonzug APQB ist nun ăźberschlagenŇ. Fźr die Winkel gilt:
5 Ausblick
Die folgenden Figuren zeigen die Situation bei Viertelung und Siebtelung der Kreisbšgen.
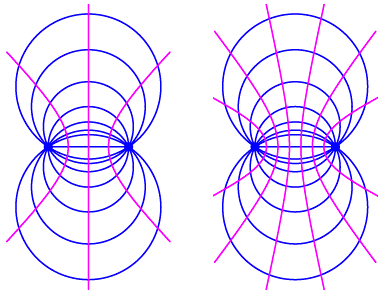
Teilungen durch 4 und durch 7
Die Kurven sehen zwar wie Hyperbeln aus, sind aber im Allgemeinen keine.