1 Worum geht es?

Mit einer Zick-Zack-Figur im Winkelfeld kann ein Winkel im Limes gedrittelt werden.

2 Die Zick-Zack-Figur

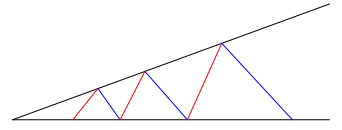
Abb. 1: Zick-Zack-Figur

Die erste rote Linie (links) im Winkelfeld kann beliebig gelegt werden. Die anschließende blaue Linie ist die Winkelhalbierende des durch die rote Linie und die Oberkante des Winkelfeldes gebildeten Winkels. Die anschließende rote Linie ist die Winkelhalbierende des durch die blaue Linie und die Unterkante des Winkelfeldes gebildeten Winkels. Und so weiter und so fort.

3 Faltvorgehen

Das Winkelfeld aus Papier wird zunächst einmal beliebig nach oben gefaltet und dann wieder zurückgefaltet. Das ergibt die erste rote Linie als Faltlinie. Die anschließende blaue Winkelhalbierende kann durch Anlegen der Oberkante des Winkelfeldes an die rote Linie erfaltet werden. Die anschließende rote Winkelhalbierende ergibt sich durch Anlegen der Unterkante des Winkelfeldes an die blaue Linie. Und so weiter und so fort.

4 Bezeichnungen

Der Winkel definiert das Winkelfeld (Abb. 2). Mit dem Startwinkel wird die erste rote Linie festgelegt.

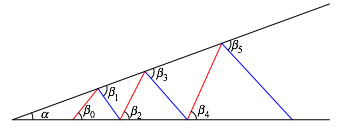
Abb. 2: Bezeichnungen

5 Rekursion

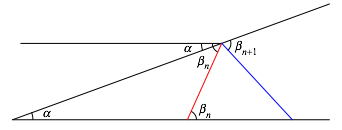
Abb. 3: Rekursion

Wir arbeiten mit Wechselwinkeln an Parallelen gemäß Abbildung 3. Der zu halbierende Winkel ist der Ergänzungswinkel von auf den gestreckten Winkel . Daher ist:

(1)

Wie groß ist ?

6 Heuristisches Vorgehen: Lilo

Wir nehmen an, dass für den Grenzwert die Rekursion (1) stabil ist (Lilo: Limit in, limit out), also:

(2)

Aus (2) ergibt sich die Vermutung:

(3)

Es erscheint die Drittelung des Winkels .

7 Beweis

Wir führen als neue Folge die Abweichung vom vermuteten Grenzwert (3) ein:

(4)

Nun setzen wir (4) in die Rekursion (1) ein:

(5)

Beim Umformen fällt vieles weg, und es bleibt:

(6)

Die Abweichungen vom vermuteten Grenzwert bilden also eine Nullfolge. Damit ist die Vermutung (3) bewiesen.

8 Visualisierung

In der Vermutung (3) erscheint zusätzlich zum Drittelwinkel der Winkel . Dies ist ein Innenwinkel des gleichseitigen Dreiecks. Durch Einfügen von gleichseitigen Dreiecken können wir diesen Zusatzterm „eliminieren“ (Abb. 4).