Hans Walser, [20180802]
Winkeldrittelung
Idee: Jo Niemeyer, Berlin
1
Worum es geht
Die Winkeldrittelung ist — zusammen mit der Wźrfelverdoppelung und der Quadratur des Kreises — eines der drei klassischen Probleme, die mit Zirkel und Lineal nicht lšsbar sind. Wir besprechen eine Einschiebelšsung mit Quadraten oder Rechtecken. Die Lšsung ist verwandt mit dem ăTomahawkŇ-Verfahren.
2 Vorgehen
Wir beginnen mit einem gegebenen Winkel (Abb. 1). Der Winkel soll nicht zu klein sein (źber das Vorgehen bei kleinen Winkeln siehe Abschnitt 4).

Abb. 1: Der zu drittelnde Winkel
Als Hilfsmittel benštigen wir zwei Quadrate aus transparentem Material mit je einer Mittelparallele (Abb. 2). Bei transparentem Papier erhalten wir die Mittelparallele durch Falten.

Abb. 2: Zwei transparente Quadrate mit Mittellinie
Wir legen eines der beiden Quadrate an einen der Schenkel an gemŠ§ Abbildung 3. Die Mittellinie des Quadrates ist parallel zum Schenkel.

Abb. 3: Anlegen des ersten Quadrates
Das zweite Quadrat schieben wir nun so ein, dass eine Quadratecke auf dem anderen Winkelschenkel liegt, die bezźglich der Mittellinie gespiegelte Quadratecke auf der Mittellinie des ersten Quadrates und die Mittellinie selbst durch den Scheitelpunkt verlŠuft (Abb. 4).
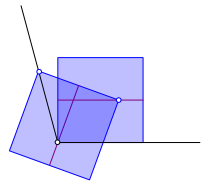
Abb. 4: Einschieben des zweiten Quadrates
Die Mittellinie des zweiten Quadrates ist eine der beiden Winkeldrittelungslinien (Abb. 5).
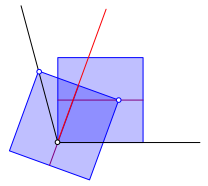
Abb. 5: Die Mittellinie drittelt den Winkel
Die zweite Winkeldrittelungslinie finden wir als Verbindungslinie des Scheitels mit dem Einschiebepunkt auf der Mittellinie des ersten Quadrates (Abb. 6).
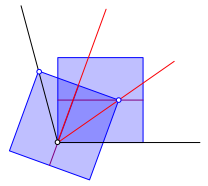
Abb. 6: Zweite Winkeldrittelungslinie
Die Abbildung 7 zeigt den gedrittelten Winkel.
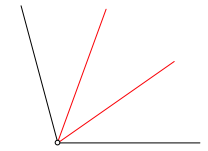
Abb. 7: Gedrittelter Winkel
3 Beweis der Winkeldrittelung
Fźr den Beweis verwenden wir die drei in die Figur eingezeichneten rechtwinkligen Dreiecke gemŠ§ Abbildung 8. Diese drei Dreiecke sind kongruent.
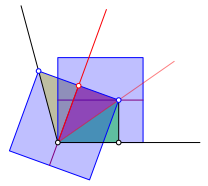
Abb. 8: Beweisfigur
Das gelbe und das rote Dreieck sind spiegelbildlich und daher kongruent. Das rote und das grźne Dreieck haben je einen rechten Winkel, gleich gro§e (in der Abb. 8 kurze) Katheten (halbe SeitenlŠnge der Quadrate) und die Hypotenuse gemeinsam. Sie sind daher kongruent. Also sind alle drei Dreiecke kongruent. Am Scheitelpunkt des Ausgangswinkels haben wir nun drei gleiche Winkel.
4 Kleine Winkel
Bei Winkeln kleiner als
![]()
mźssen wir mit entsprechend ăverlŠngertenŇ Quadraten, also Rechtecken, arbeiten (Abb. 9). Der Beweis geht analog.
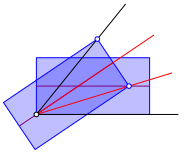
Abb. 9: Winkeldrittelung bei kleinen Winkeln
Websites
Hans Walser: Winkeldrittelung (Abgerufen 02.08.2018):
www.walser-h-m.ch/hans/Miniaturen/W/Winkeldrittelung/Winkeldrittelung.htm