Hans Walser, [20180806]

Winkeldrittelung

Anregung: Jo Niemeyer, Berlin

1 Worum es geht

Die Winkeldrittelung ist — zusammen mit der Würfelverdoppelung und der Quadratur des Kreises — eines der drei klassischen Probleme, die mit Zirkel und Lineal nicht lösbar sind. Wir besprechen eine Lösung mit Hilfe einer Kurve vierten Grades. Die Kurve hat zudem einige lustige elementargeometrische Eigenschaften.

Hintergrund sind die Lösung [1] sowie das Tomahawk-Verfahren zur Winkeldrittelung.

2 Die Kurve

Wir arbeiten mit der Kurve (Abb. 1 und 2) mit der Gleichung:

(1)

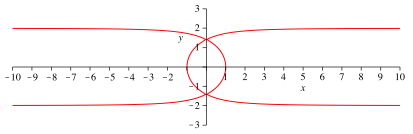
Abb. 1: Die Kurve

Da wir in (1) nur geraden Exponenten haben, sind die Koordinatenachsen auch Symmtrieachsen.

Die Abbildung 2 zeigt einen vergrößerten Ausschnitt.

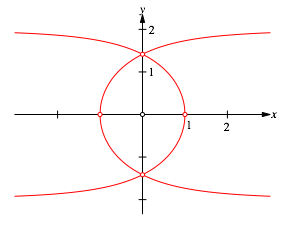
Abb. 2: Vergrößerter Ausschnitt

3 Eigenschaften der Kurve

3.1 Asymptoten

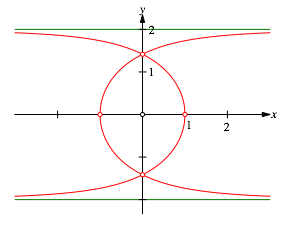
Abb. 3: Asymptoten

Die Kurve hat die beiden Asymptoten y = ±2 (Abb. 3).

3.2 Scheitelkrümmung

Die Scheitelkrümmung in den Punkten (±1, 0) ist null. Wir kennen das von der Scheitelkrümmung der Parabel vierten Grades.

3.3 DIN-Rechteck

Das Zweieck lässt sich in ein Rechteck mit dem Seitenverhältnis , ein DIN-Rechteck also, einspannen (Abb. 4).

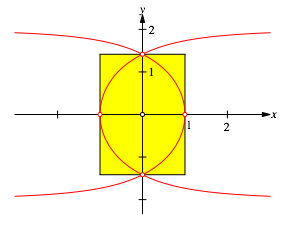
Abb. 4: DIN-Rechteck

Über das DIN-Format siehe Walser (2013).

3.4 Sechseck

Wir können ein regelmäßiges Sechseck in die Figur einpassen (Abb. 5).

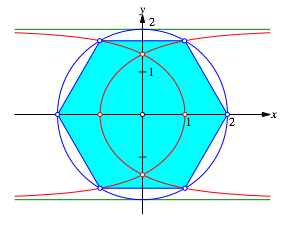
Abb. 5: Regelmäßiges Sechseck

4 Winkeldrittelung

4.1 Vorgehen

Wir legen den zu drittelnden Winkel so in die Figur, dass der Scheitel auf den Ursprung zu liegen kommt und der eine Schenkel auf die positive x-Achse (Abb. 6).

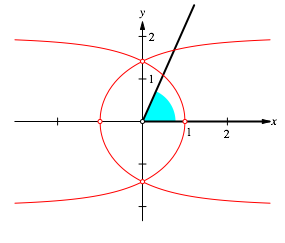
Abb. 6: Disposition

Der andere Schenkel sei nach oben gerichtet. Zu diesem anderen Schenkel zeichnen wir eine Parallele im Abstand 1 (Abb. 7). Diese Parallele schneiden wir mit dem nach oben rechts gehenden Ast unserer Kurve.

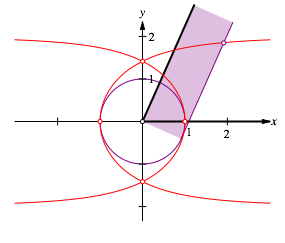
Abb. 7: Parallele im Abstand 1

Der Strahl vom Scheitel (Ursprung) durch diesen Schnittpunkt drittelt den gegebenen Winkel (Abb. 8).

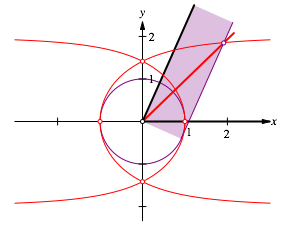
Abb. 8: Winkeldrittelung

4.2 Begründung

Zur Begründung erfinden wir unsere Kurve neu. Für zeichnen wir auf der positiven x-Achse den Punkt M(t, 0) (Abb. 9).

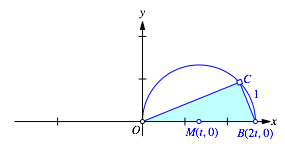
Abb. 9: Neukonstruktion

Diesen Punkt nehmen wir als Zentrum eines Thaleskreises durch den Ursprung O und ergänzen zum rechtwinkligen Dreieck OBC so dass die Kathete BC die Länge 1 hat. Daher die Bedingung .

Nun spiegeln wir den Punkt B an C und erhalten den Spiegelpunkt D (Abb. 10).

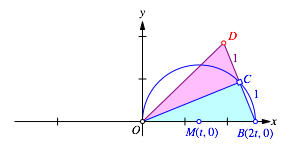
Abb. 10: Spiegeln

In der Abbildung 11 ist die Ortslinie des Punktes D bei Variation des Parameters t eingezeichnet.

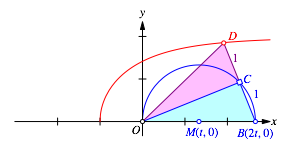
Abb. 11: Ortslinie

Wir vermuten, dass diese Ortslinie ein Ast der Kurve der Abbildungen 1 und 2 ist. Wir werden das im nächsten Abschnitt beweisen.

Vorerst aber: Die Abbildung 12 zeigt die mit dieser Ortslinie analog zur den Abbildungen 6, 7 und 8 Konstruktion. Die Winkeldrittelung wird nun offensichtlich, da wir drei kongruente rechtwinklige Dreiecke haben.

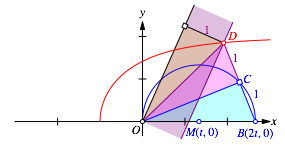
Abb. 12: Konstruktion

4.3 Umrechnung der Parameterdarstellung

Die Ortslinie gemäß der Abbildung 11 hat folgende Parameterdarstellung:

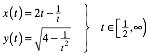(2)

Die Herleitung benötigt den Kathetensatz und die Linearität.

Wir haben zu zeigen, dass die Parameterdarstellung (2) zur Gleichung (1) führt. Durch Quadrieren erhalten wir:

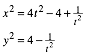(3)

Durch dieses Quadrieren entstehen die „falschen Lösungen“ (die drei weiteren Äste der Kurve). Aus (3) folgt:

(4)

Dies können wir in die untere Zeile von (3) einsetzen und erhalten nach kleinen Umformungen die Gleichung (1).

Websites

[1] Hans Walser: Winkeldrittelung (Abgerufen 07.08.2018):

www.walser-h-m.ch/hans/Miniaturen/W/Winkeldrittelung2/Winkeldrittelung2.htm

[2] Hans Walser: Winkeldrittelung (Abgerufen 02.08.2018):

www.walser-h-m.ch/hans/Miniaturen/W/Winkeldrittelung/Winkeldrittelung.htm

Literatur

Walser, Hans (2013): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-69-1.