Hans Walser, [20070512c], [20190924]

Winkeldrittelung

Aus [Brooks 2007].

Es handelt sich um ein Einschiebeverfahren, dabei wird ein rechter Winkel eingeschoben.

Zunächst ergänzen wir den gegebenen Winkel gemäß Figur; dabei ist D der Mittelpunkt der Strecke BC. Die Strecke DE ist das Lot auf den Schenkel AB.

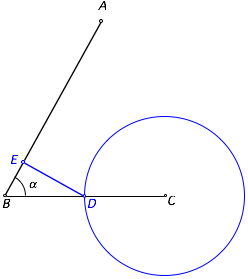
Ergänzung des gegebenen Winkels

Für spätere Berechnung wollen wir annehmen, dass der Kreis den Radius 1 hat.

Nun schieben wir einen rechten Winkel so ein, dass ein Schenkel durch B verläuft, der Scheitel F auf der Strecke ED liegt und der andere Schenkel den Kreis berührt.

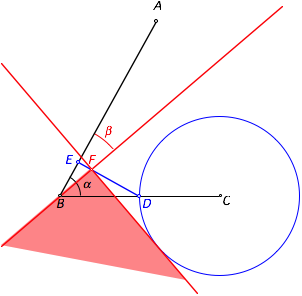
Einschieben des rechten Winkels

Dann ist .

Begründung: Wir ergänzen die Figur; dabei ist BCIF ein Parallelogramm mit der Langseite 2 und dem spitzen Winkel .

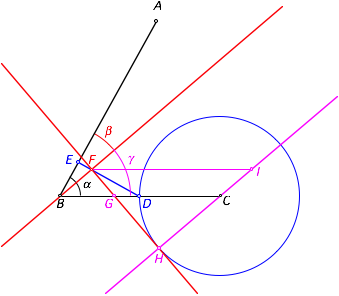
Beweisfigur

Im einzelnen gilt dann:

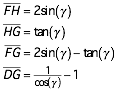
Im Dreieck DFG ergibt der Sinussatz:

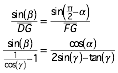
Wegen ergibt sich schließlich:

Wir lösen diese Gleichung nach auf. CAS (MuPAD) liefert als einzige sinnvolle Lösung :

glg:=sin(b)/(1/cos(g)-1)=cos(b+g)/(2*sin(g)-tan(g)):

solve(glg, g);

Somit ist .

Literatur

[Brooks 2007] Brooks, David Alan: A New Method of Trisection. The College Mathematics Journal. Vol. 38, No. 2, March 2007, p. 78-81.

Websites

Hans Walser: Winkeldrittelung mit Zykloiden

www.walser-h-m.ch/hans/Miniaturen/W/Winkeldrittelung8/Winkeldrittelung8.htm

Hans Walser: Winkeldrittelung mit Hyperbel

www.walser-h-m.ch/hans/Miniaturen/W/Winkeldrittelung7/Winkeldrittelung7.htm

Hans Walser: Winkeldrittelung mit Lemniskate

www.walser-h-m.ch/hans/Miniaturen/W/Winkeldrittelung5/Winkeldrittelung5.htm

Hans Walser: Winkeldrittelung

www.walser-h-m.ch/hans/Miniaturen/W/Winkeldrittelung4/Winkeldrittelung4.htm

Hans Walser: Winkeldrittelung

www.walser-h-m.ch/hans/Miniaturen/W/Winkeldrittelung3/Winkeldrittelung3.htm

Hans Walser: Winkeldrittelung

www.walser-h-m.ch/hans/Miniaturen/W/Winkeldrittelung2/Winkeldrittelung2.htm

Hans Walser: Winkeldrittelung

www.walser-h-m.ch/hans/Miniaturen/W/Winkeldrittelung/Winkeldrittelung.htm