Hans Walser, [20140506]

Winkelhaken

1 Worum geht es?

Es wird ein Einschiebe-Verfahren gezeigt, wie zu einer natürlichen Zahl n und einer positiven reellen Zahl c mit Hilfe von n Winkelhaken die n-te Wurzel bestimmt werden kann. Der Winkel des Winkelhakens kann beliebig gewählt werden. Zur Thematik Winkelhaken siehe (Stowasser, 1981).

2 Vorgehen

Pour fixer les idées wählen wir und oder einfacher komplex und . Ebenso wählen wir einen Winkel für den Winkelhaken.

Es wird im Folgenden exemplarisch der Fall n = 5 dargestellt.

2.1 Fächer

Wir zeichnen einen n-Fächer mit dem Scheitel O und dem Fächerwinkel so, dass der Start-Strahl durch verläuft (Abb. 1).

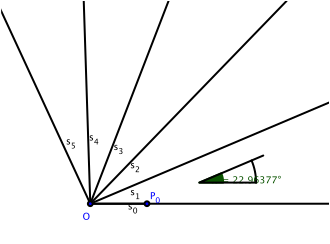
Abb. 1: Fächer

2.2 Der Radikand

Wir zeichnen auf dem letzten Strahl den Punkt C im Abstand des Radikanden c von O ein (Abb. 2).

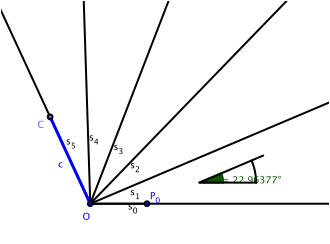
Abb. 2: Radikand c

2.3 Der erste Winkelhaken wird eingepasst

Auf dem Strahl wählen wir einen Punkt und passen einen Winkelhaken gemäß Abbildung 3 ein. Er hat seine Spitze in und einen Schenkel durch

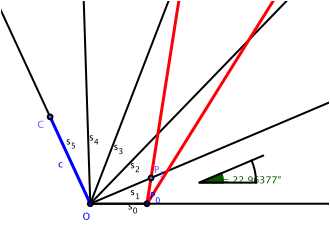
Abb. 3: Winkelhaken

2.4 Weitere Winkelhaken

Und nun passen wir weitere Winkelhaken ein gemäß Abbildung 4.

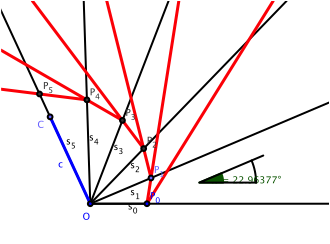
Abb. 4: Weitere Winkelhaken

Es wäre nun schön gewesen, wenn wir mit (in unserem Beispiel also ) gerade den Punkt C getüpft hätten.

Wir haben einen Fehlschuss getan wie der Vikari, der beim Mittagessen meinte, die Leute seien wegen seiner Predigt so zahlreich in die Kirche gekommen. Worauf die Pfarrerstochter bemerkte, die Leute seien gekommen, um die junge Frau des Jakobli Jowäger zu besichtigen.

Wir versuchen, den Fehlschuss zu justieren, indem wir bewegen. Hier kommt das Einpassen ins Spiel.

2.5 Zweiter Versuch

Wir haben also verschoben (Abb. 5). Der Abstand zu O wurde verkleinert.

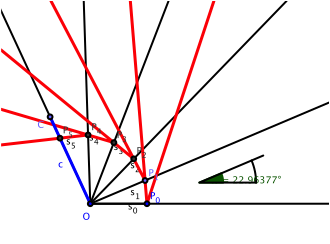
Abb. 5: Zweiter Versuch

Au weia, jetzt sind wir auf der anderen Seite falsch.

2.6 Augen und Hände

Beim Vorgehen mit realen Winkelhaken, etwa aus Papier herausgeschnittenen Sektoren, benötigen wir n Hände (für jeden Winkelhaken eine) sowie Augen, um die Punkte zu beobachten.

Unter Verwendung von DGS (dynamische Geometrie-Software) müssen wir nur noch den einen Punkt bewegen (eine Hand an der Maus) und unser Augenmerk auf richten. Ein Lob auf die DGS.

Es gibt auch mechanische Modelle (Gleit- und Gelenkgeometrie) zur Darstellung des Sachverhaltes. Auch dort haben wir einen freien Justierparameter.

2.7 Zielschuss?

Der nächste Versuch sieht besser aus (Abb. 6).

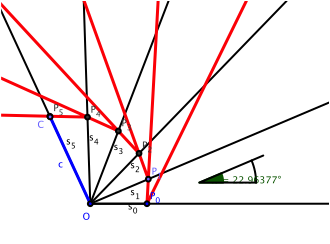
Abb. 6: Zielschuss?

Wenn jetzt tatsächlich wäre, dann hätten die Punkte von O den Abstand:

Insbesondere wäre .

Da allerdings nur optisch eingepasst ist und nicht eingerastet, ist die Sache nicht exakt im Sinne euklidischer Puristen.

Das Einrasten, also die Identifizierung mit C, ist in DGS nicht möglich, da DGS ein Abbild der euklidischen Geometrie ist. Wenn man’s trotzdem versucht, kommt eine Fehlermeldung.

3 Hintergrund

Die Punkte liegen auf einer logarithmischen Spiralen.

Mit der Bezeichnung ist in komplexer Schreibweise:

Weiter ist . Aus der Identifizierung ergäbe sich:

Alles im Konjunktiv, da nicht „exakt“ im Euklidischen Sinne.

4 Didaktisches

Das Einschiebe-Verfahren kann also Probleme lösen, welche mit Zirkel und Lineal und damit auch mit DGS nicht lösbar sind.

Andererseits sind die Einschiebe-Verfahren außer in einfachen Fällen ohne die Hilfe von DGS nicht praktikabel.

In unserem Beispiel leistet DGS wenigstens die Vorwärtskonstruktion von auf . Wir bräuchten eigentlich die Rückwärtskonstruktion von auf . Das Einpass-Verfahren ist eine Probierverfahren, das aber dank DGS technisch erleichtert wird.

Literatur

Stowasser, R. J. K. (1981): Erkundung eines geometrischen Problemfeldes – mit den Augen eines Lehrers. In B. Artmann (Hrsg.), Beiträge zum Mathematikunterricht 1981, S. 96.