Hans Walser, [20190922]
Winkelhalbierung mit Parabel oder Kardioide
1 Worum geht es?
Es werden zwei Methoden vorgestellt, einen Winkel zu halbieren. Als Hilfsfiguren werden die Parabel beziehungsweise die Kardioide verwendet.
Die Methoden sind ăschšnŇ, haben aber keine praktische Bedeutung.
Die Studie gehšrt in die Kategorie ălustig aber unnźtzŇ.
2 Winkelhalbierung mit Parabel
Wir arbeiten mit einer Parabel, deren Brennpunkt und deren Leitlinie (Abb. 1).

Abb. 1: Parabel mit Brennpunkt und Leitlinie
Den zu halbierenden Winkel passen wir so ein, dass sein Scheitelpunkt im Brennpunkt der Parabel liegt und ein Schenkel auf der Symmetrieachse der Parabel (Abb. 2).
Den zweiten Winkelschenkel schneiden wir mit der Parabel.
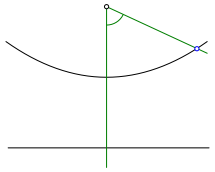
Abb. 2: Einpassen des Winkels
Vom Schnittpunkt des zweiten Schenkels mit der Parabel zeichnen wir das Lot auf die Leitlinie (Abb. 3).
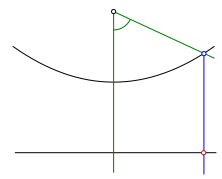
Abb. 3: Lot auf Leitlinie
Mit dem Fu§punkt des Lotes auf der Leitlinie kann die Winkelhalbierende gezeichnet werden (Abb. 4).
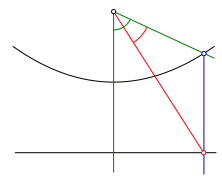
Abb. 4: Winkelhalbierende
Fźr den Beweis der Stimmigkeit der Konstruktion kann das in Abbildung 5 markierte Dreieck verwendet werden. Es ist gleichschenklig.
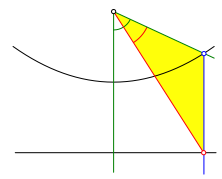
Abb. 5: Beweisfigur
3 Winkelhalbierung mit Kardioide
Die Kardioide ist die Bahn eines Kreispunktes, dessen Kreis auf einem gleich gro§en Kreis abrollt. In der Abbildung 6 sind die Kardioide und der Rollbasiskreis eingezeichnet, auf dem der Kreis mit dem Kreispunkt abrollte.

Abb. 6: Kardioide und Rollbasiskreis
Wir passen den zu halbierenden Winkel so ein, dass der Scheitel auf die EinwŠrtsspitze der Kardioide zu liegen kommt und ein Winkelschenkel auf die Symmetrieachse der Kardioide (Abb. 7). Den zweiten Schenkel schneiden wir mit der Kardioide.
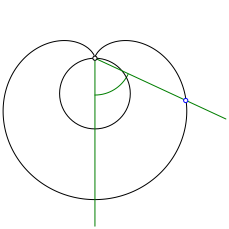
Abb. 7: Einpassen des Winkels
Nun zeichnen wir einen Kreis, welcher den ersten Schenkel im Scheitel berźhrt und durch den Schnittpunkt des zweiten Schenkels mit der Kardioide verlŠuft (Abb. 8). Diesen Kreis schneiden wir mit dem Rollbasiskreis.
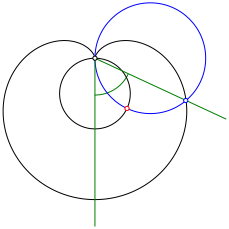
Abb. 8: Kreis
Der Schnittpunkt liegt auf der Winkelhalbierenden (Abb. 9).

Abb. 9: Winkelhalbierende
Der Beweis ergibt sich durch eine Kreisspiegelung. Es ist so, dass die Kardioide das Bild einer Parabel bei einer Kreisspiegelung ist. Daher kann die †berlegung mit der Parabel auf die Kardioide źbertragen werden.
Websites
Hans Walser: Winkelhalbierung
www.walser-h-m.ch/hans/Miniaturen/W/Winkelhalbierung/Winkelhalbierung.htm