Hans Walser, [20130822]
Winkelmessung
Anregung: Chr. D. und A. K.
1 Worum es geht
Fr die Winkelmessung wird in der Schule das Gradma§ (Degree), in der Praxis das Bogenma§ (Radian) und in der Vermessung das gon (Grad) verwendet.
Die Frage ist, was es mit dem Winkel von 1¡ beziehungsweise 1gon auf sich hat.
2 Problem der Einheit
Es ist denkbar (ich kann das aber nicht belegen), dass bei den Babyloniern die Einheit fr die Winkelmessung der Innenwinkel im gleichseitigen Dreieck war (Abb. 1).

Abb. 1: Winkeleinheit
Das gleichseitige Dreieck ist ja die einfachste Figur, die mit Zirkel und Lineal, insbesondere auch mit dem Zirkel allein, konstruiert werden kann. Da die Babylonier ein Zahlensystem auf der Basis 60 verwendeten, ist die Winkelgr§e 1¡ die erste Unterteilung der Winkeleinheit. Nachfolgenden Unterteilungen sind Minuten und Sekunden.
Wenn wir heute sagen, der Innenwinkel im gleichseitigen Dreieck messe 60¡, ist das ebenso absurd wie wenn der Euro als Geldwert von 100 Cent definiert wrde. In der Schweiz gibt es allerdings das Sprichwort: Wer den Rappen nicht ehrt, ist des Franken nicht wert.
3 Zwei Welten
Euklid verwendet als Winkeleinheit den rechten Winkel.
Es gibt offenbar in der geometrischen Tradition zwei Richtungen, zwei ãWeltenÒ sozusagen.
3.1 Kreisdenken
Stichworte:
Kreisgeometrie, gleichseitiges Dreieck, sphrische Geometrie, Unterteilung in
¡, Dreiecksraster, Hexagonalraster, ![]() , platonische Krper mit Ausnahme des Wrfels, himmlisches
Denken. Babylon.
, platonische Krper mit Ausnahme des Wrfels, himmlisches
Denken. Babylon.
3.2 Orthogonales Denken
Das orthogonale Denken basiert auf dem rechten Winkel (Abb. 2).

Abb. 2: Winkeleinheit
Stichworte: Euklid,
Faltgeometrie, Unterteilung in gon, rechtwinkliges Dreieck, Pythagoras,
Bauwesen (Aber erst musst du mir selber gebaut sein, rechtwinklig an Leib und
Seele. Nietzsche, Zarathustra),
Quadratraster, kartesisches Koordinatensystem, ![]() , Wrfel, irdisches Denken. gypten und Griechenland.
, Wrfel, irdisches Denken. gypten und Griechenland.
Didaktisches: Das orthogonale Denken ist derart verinnerlicht, dass offensichtlich falsche Figuren ãrichtigÒ, das hei§t in der Intention des Zeichners, gedeutet werden. Es findet eine Orthogonalisierung im Kopf statt.
Die Figur der Abbildung 3a wird als Wrfel interpretiert, obwohl ein Wrfel nicht annhernd so gesehen werden kann. Diese Technik des Schrgbildes ist in der Schule leider weit verbreitet. Die in der gleichen Technik des Schrgbildes eingezeichnete Innenkugel des Wrfels (Abb. 3b) wirkt verzerrt und kann nicht mehr so einfach im Kopf zurechtgebogen werden. Der Umriss der Kugel erscheint als Ellipse, was sehr unnatrlich wirkt.
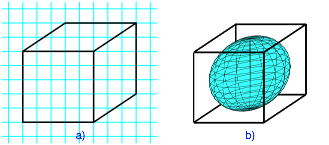
Abb. 3: Wrfel im Schrgbild
Die Abbildung 4 zeigt, wie man es besser machen knnte (Abbildung 4a basierend auf LEGO¨ CITY, Bauanleitung 3178_1, S. 5). Es handelt sich um eine so genannte Normalaxonometrie. Hier sind allerdings nun gar keine rechten Winkel sichtbar, wir sind ebenfalls auf die Orthogonalisierung im Kopf angewiesen. Dafr ist die Innenkugel des Wrfels schn rund (Abb. 4b).
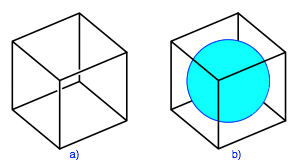
Abb. 4: Wrfel in orthografischer Darstellung (Normalaxonometrie)
4 Alltag, Wissenschaft und Vermessung
Die Winkelunterteilung mit 360¡ fr den Vollwinkel wird in der Schule und fr die Schule unterrichtet. Sie hat daher im umgangssprachlichen Alltag eine gewisse Bedeutung.
Die Wissenschaft arbeitet mit dem Bogenma§, die Vermessung mit der Unterteilung des Vollwinkels in 400gon.
Gelegentlich findet man
noch andere Ma§e, etwa die Unterteilung des Vollwinkels in 32 oder 64 oder 6400
Teile (Kompassrose mit Stricheinteilung). Wegen ![]() haben wir damit
eine grobe Approximation an das Bogenma§.
haben wir damit
eine grobe Approximation an das Bogenma§.
5 Konstruierbarkeit
5.1 Grad
Der Innenwinkel im gleichseitigen Dreieck ist mit Zirkel (und Lineal) sehr einfach konstruierbar, aber der Winkel von 1¡ ist mit Zirkel und Lineal nicht konstruierbar. Mit 1¡ wre auch 40¡ konstruierbar und damit das regelm§ige Neuneck.
Ein Winkel von 3¡ ist auf verschiedene Weisen konstruierbar. Man kann etwa zu 60¡ einen Viertel davon addieren, hat dann also 75¡, und davon den Zentriwinkel 72¡ des regelm§igen Fnfeckes subtrahieren.
Damit sind auch alle
Vielfachen von 3¡ konstruierbar. Hingegen ist ein Winkel von ![]() , nicht konstruierbar, weil man sonst durch Differenzbildung
einen Winkel von 1¡ konstruieren knnte.
, nicht konstruierbar, weil man sonst durch Differenzbildung
einen Winkel von 1¡ konstruieren knnte.
Bei den Winkeln mit
ganzzahligem Gradma§ sind also genau die Winkel von der Form ![]() , konstruierbar.
, konstruierbar.
5.2 Gon
Der rechte Winkel ist mit Zirkel und Lineal konstruierbar, aber der Winkel von 1gon ist mit Zirkel und Lineal nicht konstruierbar. Mit 1gon wre auch 16gon konstruierbar und damit das regelm§ige 25-Eck.
Damit ist auch ein Winkel von 2gon nicht konstruierbar.
Einen Winkel von 5gon erhalten wir durch mehrfaches Halbieren des Zentriwinkels 80gon des regelm§igen Fnfeckes.
Damit
sind auch alle Vielfachen von 5gon konstruierbar. Hingegen sind Winkel von der
Form ![]() , oder
, oder ![]() , nicht konstruierbar, weil man sonst durch Differenzbildung
Winkel von 1gon oder 2gon konstruieren knnte.
, nicht konstruierbar, weil man sonst durch Differenzbildung
Winkel von 1gon oder 2gon konstruieren knnte.
Unter
den Winkeln mit ganzzahligem gon-Ma§ sind also genau die Winkel von der Form ![]() , konstruierbar.
, konstruierbar.