Hans Walser, [20160518]
Winkelprobleme
1 Worum geht es?
Es wird eine Serie von Winkelproblemen mit unterschiedlichem Schwierigkeitsgrad vorgestellt.
2 Die Probleme
Die Abbildungen 1a bis 1h zeigen die Probleme. Wie gro§ ist jeweils der rot markierte Winkel?


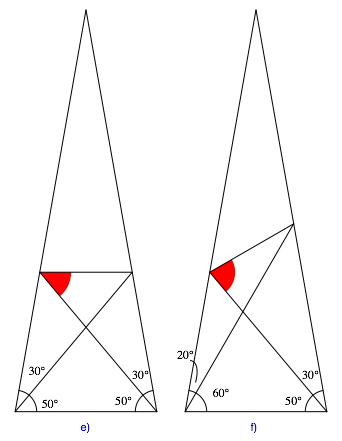
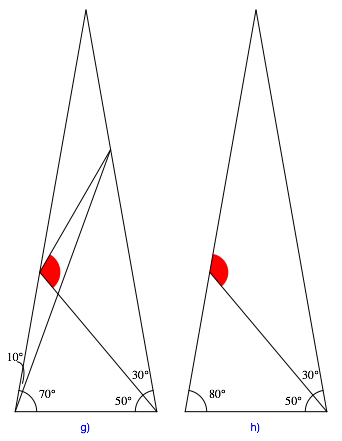
Abb. 1: Wie gro§ ist der rote Winkel?
3 Resultate
Experiment mit DGS ergibt (Tab. 1):
|
Aufgabe |
1a |
1b |
1c |
1d |
1e |
1f |
1g |
1h |
|
Winkel |
4.37370¡ |
10¡ |
17.87799¡ |
30¡ |
50¡ |
80¡ |
110¡ |
130¡ |
Tab. 1: Ergebnisse
Auffallend sind die vielen ãschnenÒ Ergebnisse. Wie lassen sich diese beweisen?
4 Bearbeitungen
Die ãhsslichenÒ Beispiele a und c lassen wir weg.
Die Beispiele 1d (Drachenviereck), 1e (Gleichschenkliges Trapez) und 1h (Au§enwinkel im Dreieck) sind trivial.
Bleiben die spannenden Beispiele 1b, 1f und 1g.
4.1 Der Fall 1b
Aus Platzspar-Grnden ist in der Abbildung 2 nur der relevante Teil der Abbildung 1b gezeichnet.
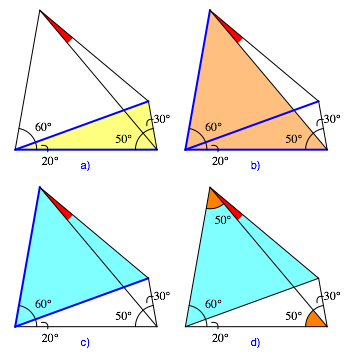
Abb. 2: Beweiskette fr den Fall 1b
Das in der Abbildung 2a markiert gelbe Dreieck hat die Winkel 20¡ und 80¡. Der dritte Winkel misst daher auch 80¡. Das gelbe Dreieck ist gleichschenklig, die blauen Strecken sind gleich lang.
Das in der Abbildung 2b markierte orange Dreieck hat die Winkel 80¡ und 50¡. Der dritte Winkel misst daher auch 50¡. Das orange Dreieck ist gleichschenklig, und wir haben eine dritte blaue Strecke gleicher Lnge.
Das in der Abbildung 2c markierte hellblaue Dreieck hat zwei gleich lange Seiten und den eingeschlossenen Winkel 60¡. Es ist also gleichseitig, auch die beiden anderen Winkel messen 60¡.
Der gesuchte rote Winkel ist nun die Differenz eines 60¡-Winkels des hellblauen gleichseitigen Dreiecks minus einem 50¡-Winkel des orangen Dreiecks.
Der rote Winkel misst also 10¡.
4.2 Der Fall 1f
Eine ausfhrliche Bearbeitung des Falles 1f hier.
Die Figur der Abbildung 1f lsst sich in einen regelm§igen Stern mit neun Spitzen einpassen (Abb. 3).

Abb. 3: Stern mit neun Spitzen
Damit lsst sich zunchst der lila markierte Winkel zu 30¡ berechnen und schlie§lich der rote Winkel zu 80¡.
4.3 Der Fall 1g
Zur Vorbereitung machen wir eine kleine Faltbung (Abb. 4). Wir beginnen mit einem regelm§igen Neuneck auf einem Papier, das vorne gelb und auf der Rckseite himmelblau ist. Auf der Vorderseite zeichnen wir zwei Diagonalen ein gem§ Abbildung 4a. Diese beiden Diagonalen schneiden sich unter 20¡ (halber Zentriwinkel des regelm§igen Neunecks). Das durch die beiden Diagonalen gebildete gleichschenklige Dreieck entspricht dem Umrissdreieck der Figuren der Abbildung 1.
Nun falten wir den linken Teil des Papiers abwechslungsweise an den beiden Diagonalen. So entsteht zwischen den beiden Diagonalen eine gleichseitige Zickzacklinie. Die Seitenlnge ist gleich der Seitenlnge des Neunecks.
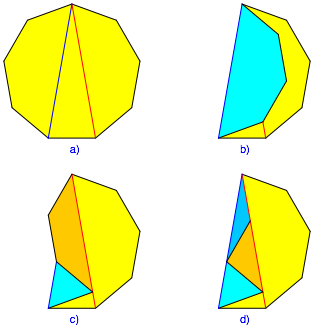
Abb. 4: Falten
Somit erhalten wir eine Folge von gleichschenkligen Dreiecken. Wir knnen deren Winkel von oben nach unten (oder von unten nach oben) berechnen. Das oberste gleichschenklige Dreieck (blau in Abb. 4d) hat die Winkel 140¡, 20¡, 20¡. Das nchste (goldgelb) hat die Winkel 100¡, 40¡, 40¡. Das nchste (himmelblau) hat die Winkel 60¡, 60¡, 60¡; es ist also gleichseitig. Das unterste (gelb) schlie§lich hat die Winkel 20¡, 80¡, 80¡.
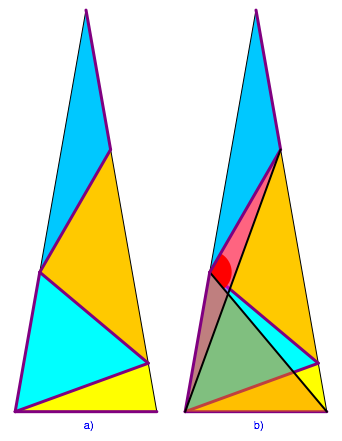
Abb. 5: Weitere gleichschenklige Dreiecke
Das himmelblaue gleichseitige Dreieck liefert uns noch eine weitere Strecke gleicher Lnge (Abb. 5a). Somit ergeben sich noch zwei weitere gleichschenklige Dreiecke, die in der Abbildung 5b mit schwarzer Grundlinie eingezeichnet sind. Das eine hat die Winkel 80¡, 50¡, 50¡. Seine Grundlinie hat zur Basis der Gesamtfigur einen Neigungswinkel 50¡. Das zweite gleichschenklige Dreieck hat die Winkel 160¡, 10¡, 10¡. Seine Grundlinie hat zur Basislinie der Gesamtfigur einen Neigungswinkel 70¡.
Das ist nun aber genau die Disposition der Figur der Abbildung 1g. Der gesuchte rote Winkel ist die Differenz 160¡ – 50¡ = 110¡.