Hans Walser, [20221216]

Winkelpuzzle

1 Worum geht es?

Kombinatorisches Spiel mit Winkelfiguren

2 Winkel in der Ebene

Wir arbeiten mit vier Winkeln (Abb. 1). Jeder einzelne Winkel ist aus drei Quadraten zusammengesetzt.

Abb. 1: Vier Winkel

Nun versuchen wir, die vier Winkel zu einem längenmäßig doppelt so großen Winkel (Abb. 2) zusammenzusetzen.

Abb. 2: Großer Winkel

Es gibt (bis auf Permutationen der Farben) genau eine Lösung (Abb. 3).

Abb. 3: Die Lösung

3 Winkel im Raum

Nun versuchen wir dasselbe im Raum. Wir arbeiten mit acht Winkeln (Abb. 4), die aus je drei Würfeln zusammengesetzt sind. (Die Figuren sind in isometrischer Axonometrie gezeichnet.)

Abb. 4: Acht Winkel im Raum

Die acht Winkel sollen zu einem längenmäßig doppelt so großen Winkel (Abb. 5) zusammengesetzt werden.

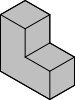
Abb. 5: Großer Winkel

Hier gibt es viele Lösungen. Die Abbildung 6 zeigt einige davon.

Abb. 6: Einige Lösungen

Wie viele Lösungen gibt es?

4 Hintergrund

Wir arbeiten mit einer Fallunterscheidung.

4.1 O quae duplicatio mundi

Die einfachste Lösung ergibt sich, indem wir die zweidimensionale Lösung (Abb. 3) duplizieren und die beiden Scheiben zusammenheften (Abb. 7).

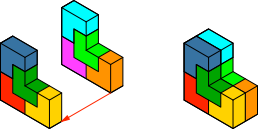
Abb. 7: Duplizieren der zweidimensionalen Lösung

Wir haben es dann mit vier „breiten“ Winkeln zu tun (Abb. 8). Man kann auch von einem grün-hellgrünen Sofa reden.

Abb. 8: Breiter Winkel. Grün-hellgrünes Sofa

Allerdings können wir zwei Winkel noch auf zwei andere Arten zu einem Sofa zusammensetzen (Abb. 9). Diese beiden Sofas sind (von den Farben abgesehen) spiegelbildlich.

Abb. 9: Weitere Sofas

Ein breiter Winkel (Sofa) kann also insgesamt auf drei Arten aus zwei Winkeln zusammengesetzt werden. In die Lösung der Abbildung 7 können wir also auf drei verschiedene Arten ein grün-hellgrünes Sofa einbauen (Abb. 10).

Abb. 10: Drei verschiedene grün-hellgrüne Sofas

Die Lösung gemäß der Abbildung 7 enthält vier Sofas. Durch Permutation der Sofas ergeben sich zunächst 3×3×3×3 = 3⁴ = 81 Lösungen.

Allerdings haben wir damit die Rechnung ohne die Symmetrie gemacht. Es kann durchaus zwei scheinbar verschiedene, in Wirklichkeit aber (abgesehen von den Farben) gleiche Lösungen geben (Abb. 11).

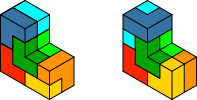
Abb. 11: Zwei gleiche Lösungen

Der große Winkel hat nämlich eine Achsensymmetrie (Abb. 12). Die Symmetrieachse verläuft durch die Mittelpunkte der beiden Gehrungskanten. Bei einer Drehung um diese Achse um 180° wird der große Winkel in sich selber übergeführt.

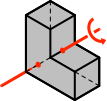
Abb. 12: Symmetrieachse

Die beiden Konfigurationen der Abbildung 11 werden durch eine Drehung um die Symmetrieachse um 180° (abgesehen von den Farben) in sich selber übergeführt. Der orange Winkel in der Konfiguration links wird zum dunkelblauen Winkel in der Konfiguration rechts.

Die beiden Sofas im Gehrungsbereich (grün-hellgrün sowie rot-magenta) sind invariant gegenüber Drehungen um 180° um die Symmetrieachse des großen Winkels. Die Achse ist auch Symmetrieachse dieser beiden Sofas.

Für unser Problem relevant sind also nur die beiden Sofas an den Enden der Schenkel des großen Winkels. Die Abbildung 13 zeigt die beiden Paare scheinbar verschiedener, in Wirklichkeit aber gleicher Lösungen.

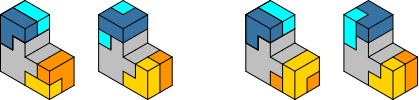
Abb. 13: Paare scheinbar verschiedener, in Wirklichkeit aber gleicher Lösungen

Im grauen Bereich haben wir nach wie vor 3×3 = 9 Lösungen.

Im Endbereich haben wir statt 3×3 = 9 nur noch 7 Lösungen (zwei fallen weg).

Somit ergeben sich insgesamt 3×3×7 = 63 Lösungen.

4.2 Turm mit Sockel

Die folgenden Lösungen sind bezüglich der Achse der Abbildung 12 asymmetrisch. Es besteht also keine Gefahr, dass Lösungen mehrfach gezählt werden.

4.2.1 Sockel

Wir beginnen mit dem Sockel. Aus zwei Winkeln setzen wir einen 2×3×1-Quader zusammen (Abb. 14). An einem Ende setzen wir einen breiten Winkel an. Dies ist der Sockel. Wenn wir dann noch einen Turm (2×2×3-Quader) aufsetzen, ergibt sich ein großer Winkel gemäß Abbildung 5.

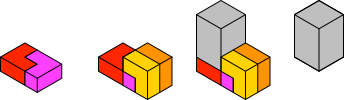
Abb. 14: Sockel

Den 2×3×1-Quader können wir an einer senkrechten Mittelnormalebene spiegeln. Für den breiten Winkel haben wir drei Lösungen. Somit gibt es 2•3 = 6 Möglichkeiten, den Sockel zu bauen. Im Sockel werden vier Winkel verbaut.

4.2.2 Turm

Die restlichen vier Winkel müssen zum Turm verbaut werden.

4.2.2.1 Sofas

Die einfachste Lösung besteht darin, zunächst aus zwei Winkeln einen 1×2×3-Quader zu bauen (Abb. 15) und diesen mit einem Duplikat zu verheften.

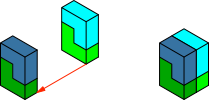
Abb. 15: Duplikation eines Quaders

Damit sind zwei breite Winkel (Sofas) im Spiel. Da wir diese auf je 3 Arten bauen können, ergeben sich zunächst 3•3 = 9 Möglichkeiten. Die Abbildung 16 zeigt ein Beispiel.

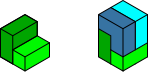
Abb. 16: Verschieden gebaute breite Winkel (Sofas)

Nun können wir aber einen so gebauten Turm vor dem Aufsetzen auf den Sockel noch mit Vierteldrehungen um seine senkrechte Achse verdrehen. Wir haben also insgesamt 6•9•4 = 216 Möglichkeiten, auf diese Art einen großen Winkel zu bauen.

4.2.2.2 Verdrehte Quader

Wir verdrehen den einen der beiden 1×2×3-Quader vor dem Verheften mit dem anderen um seine senkrechte Mittelachse um 180° (Abb. 17). Der entstehende Turm hat eine Achsensymmetrie mit der senkrechten Mittelachse als Symmetrieachse. Wir können also vor dem Aufsetzen auf den Sockel lediglich um 90° drehen, nicht aber um 180°.

Abb. 17: Verdrehen eines Quaders

Hingegen gibt es zu jedem so gebauten Turm einen spiegelbildlichen Turm (Abb. 18).

Abb. 18: Turm und spiegelbildlicher Turm

Somit haben wir insgesamt 6•(2+2) = 24 Möglichkeiten, auf diese Art einen großen Winkel zu bauen.

4.2.2.3 Und noch eine Lösung

Die Abbildung 19 zeigt schrittweise eine weitere Lösung, aus vier Winkeln einen Turm zu bauen. Auch dieser Turm hat eine Achsensymmetrie mit der senkrechten Mittelachse als Symmetrieachse. Wir können also vor dem Aufsetzen auf den Sockel lediglich um 90° drehen, nicht aber um 180°.

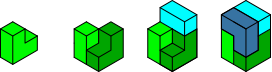
Abb. 19: Noch ein Turm

Hingegen gibt es zu jedem so gebauten Turm ebenfalls einen spiegelbildlichen Turm (Abb. 20).

Abb. 20: Spiegelbildliche Türme

Wir haben somit wieder 6•(2+2) = 24 Möglichkeiten, auf diese Art einen großen Winkel zu bauen.

4.3 Anzahl Lösungen

Sofa-Lösungen: 63

Turm mit Sockel:

Sofa-Türme: 216

Verdrehte Quader: 24

Noch eine Lösung: 24

Damit ergeben sich insgesamt 327 Lösungen.

Der Autor hofft, dass er keine Lösungen übersehen oder mehrfach gezählt hat.

5 Modellbau

Die acht Winkel der Abbildung 4 können aus je drei Flechtwürfeln als Papiermodell gebaut werden (Abb. 21).

Abb. 21: Flechtmodell

Die Abbildung 22 zeigt einen damit gebauten großen Winkel.

Abb. 22: Großer Winkel

Weblinks

Hans Walser: Quaderverachtfachung

http://www.walser-h-m.ch/hans/Miniaturen/Q/Quaderverachtfachung/Quaderverachtfachung.html

Hans Walser: Iterationen

http://www.walser-h-m.ch/hans/Miniaturen/I/Iterationen2/Iterationen2.html