Hans Walser, [20220424]

Winkelschwerpunkte

1 Ausgangslage

Es seien A[i], i = 1 .. n, n ≥ 3, die Eckpunkte eines einfach geschlossenen Polygons und alpha[i], i = 1 .. n, die zugehörigen Innenwinkel, gemessen im Bogenmaß.

Es ist:

(1) sum(alpha[i], i = 1 .. n) = (n-2)*Pi Innenwinkelsumme

(2) sum((Pi - alpha[i]), i = 1 .. n) = 2*Pi Außenwinkelsumme (von n unabhängig)

(3) sum((2*Pi - alpha[i]), i = 1 .. n) = (n + 2)*Pi Ergänzungswinkelsumme

2 Definitionen

Wir definieren folgende Winkelschwerpunkte:

(4) Wi := 1/((n-2)*Pi)*sum(alpha[i]* A[i], i = 1 .. n) Innenwinkelschwerpunkt

Wir können uns den Innenwinkelschwerpunkt als physikalischen Schwerpunkt denken, indem die Polygonecken mit den zugehörigen Innenwinkeln gewichtet werden.

(5) Wa := 1/(2*Pi) *sum((Pi - alpha[i])* A[i], i = 1 .. n) Außenwinkelschwerpunkt

(6) We := 1/((n + 2)*Pi) *sum((2*Pi - alpha[i])* A[i], i = 1 .. n) Ergänzungswinkelschwerpunkt

Ferner sei S der übliche Schwerpunkt (Eckenschwerpunkt)

(7) S := 1/n* sum(A[i], i = 1 .. n) Eckenschwerpunkt

3 Beispiele

3.1 Dreieck

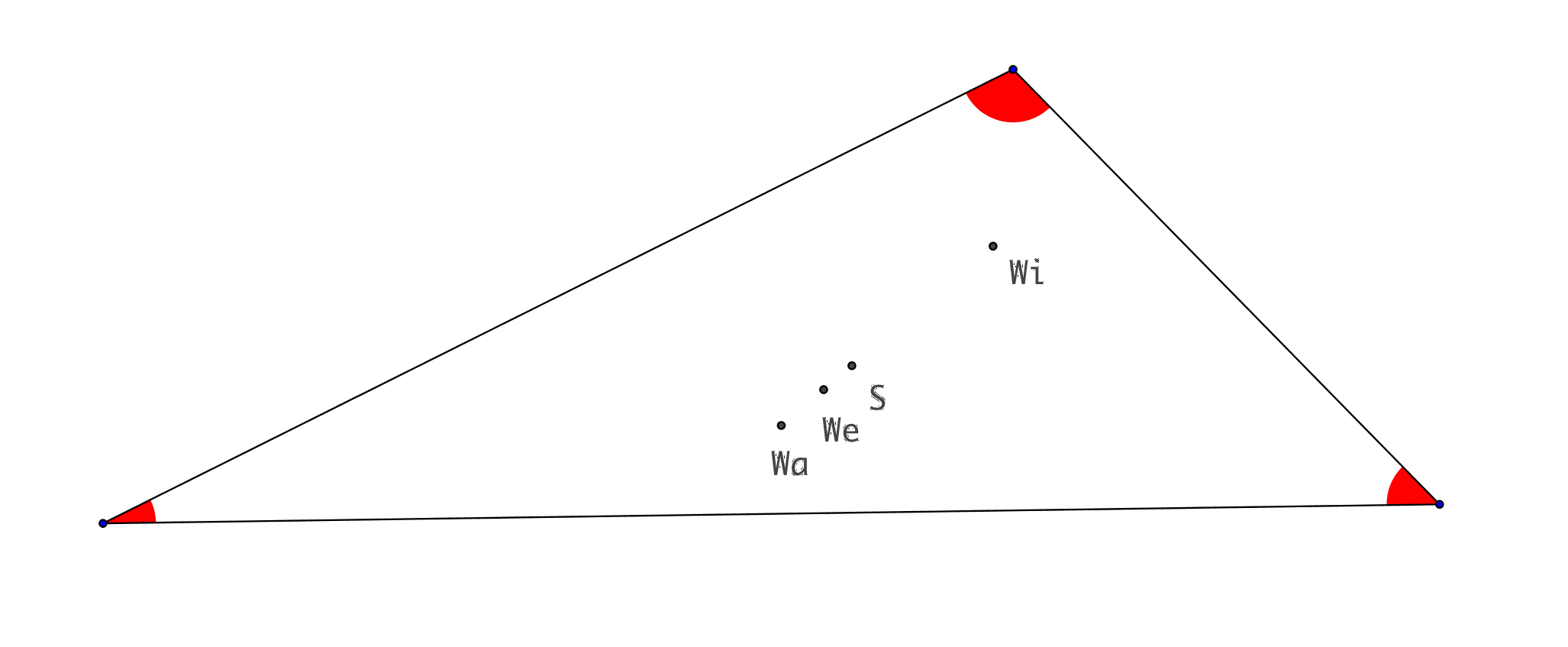
Abb. 1: Dreieck

3.2 Vierecke

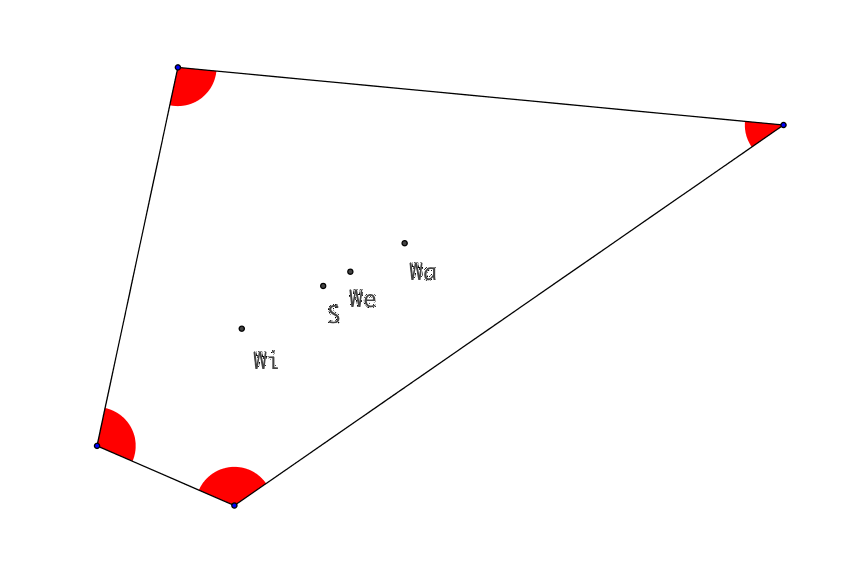
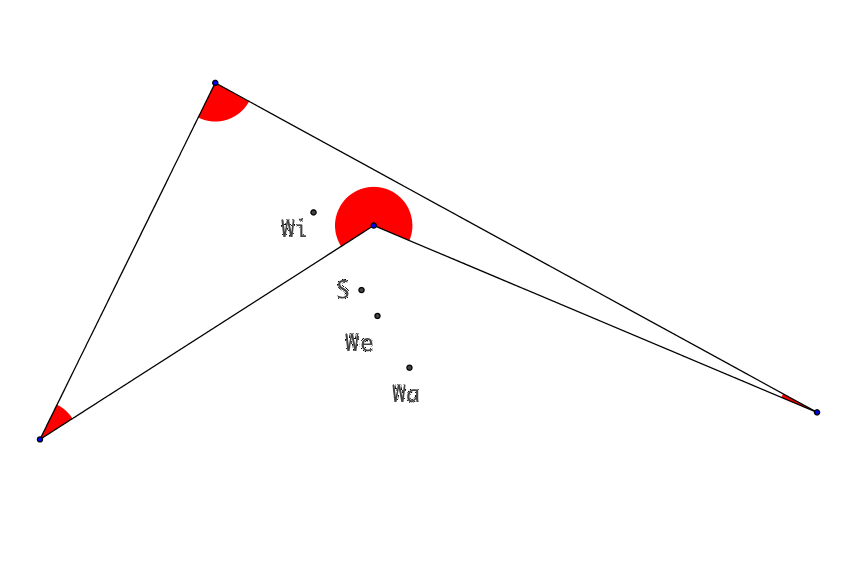
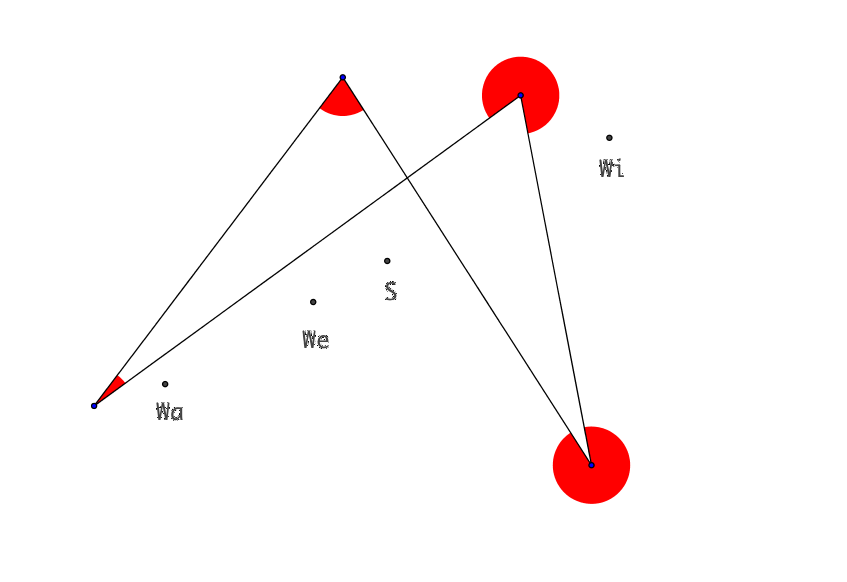
Abb. 2: Vierecke

3.3 Fünfecke

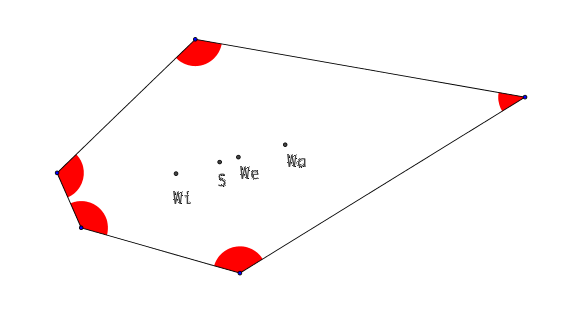
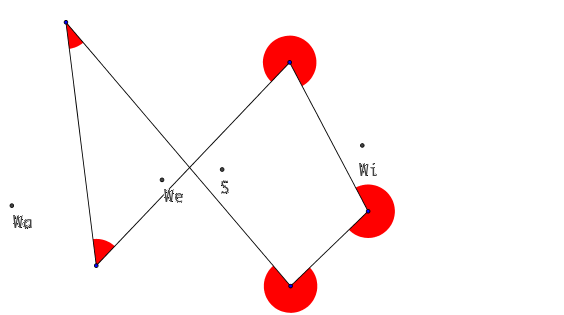
Abb. 3: Fünfecke

3.4 Sechsecke

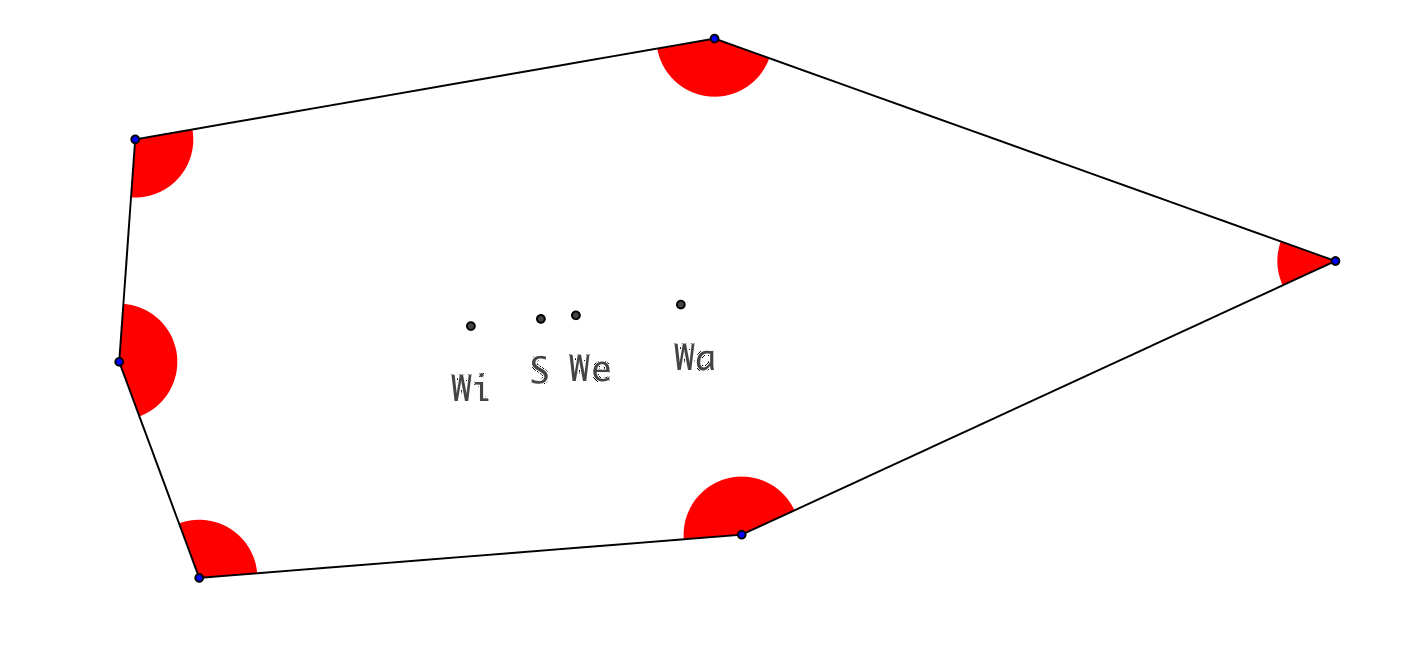
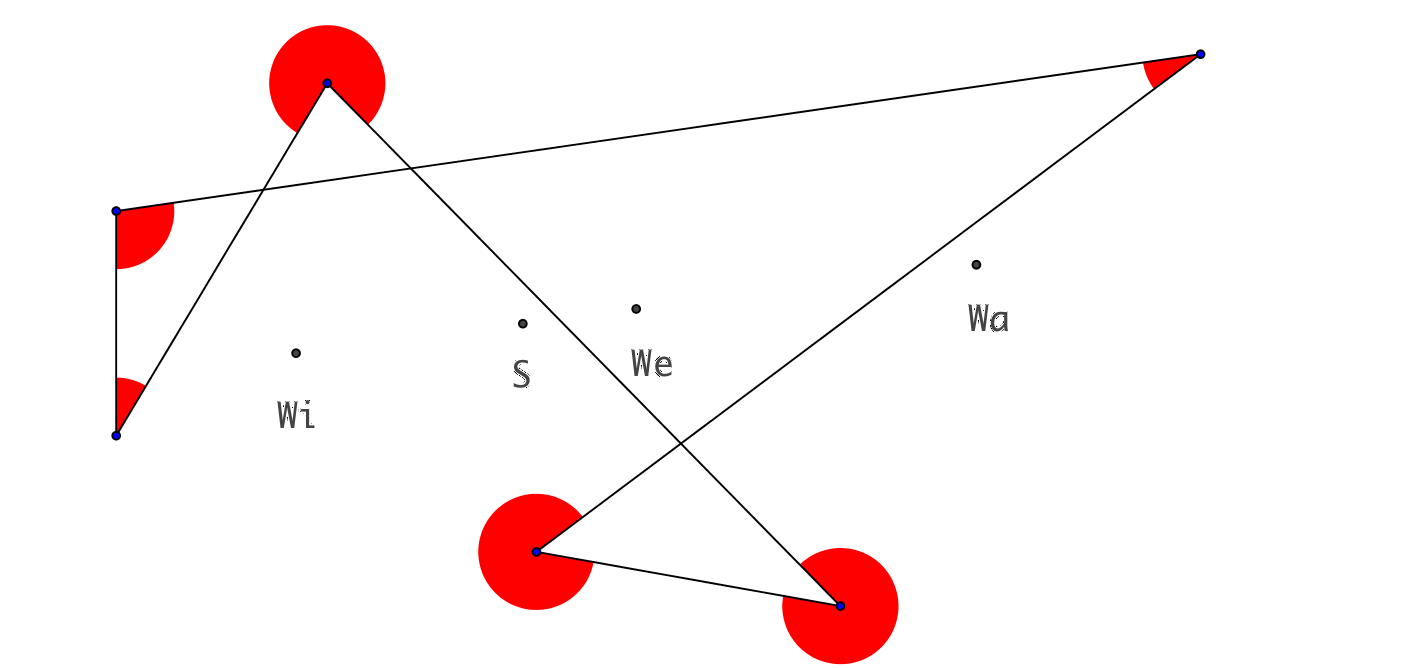
Abb. 4: Sechsecke

4 Eine Gerade

In sämtlichen Beispielen liegen die vier Punkte jeweils auf einer Geraden. Die beiden Punkte We und S liegen im Innern der Strecke WiWa.

5 Beweis für den allgemeinen Fall

Es genügt zu zeigen, dass We beziehungsweise S je eine Linearkombination von Wi und Wa sind.

Es ist:

(8) We = (n - 2)/(n + 2)*Wi + 4/(n + 2)*Wa Nachweis: (4), (5) und (6) einsetzen und rechnen

(9) S = (n – 2)/n*Wi + 2/n*Wa Nachweis: (4), (5) und (7) einsetzen und rechnen

Da alle Koeffizienten zwischen 0 und 1 liegen, liegen die beiden Punkte We und S liegen im Innern der Strecke WiWa.