Hans Walser, [20180814]
Winkelteilung
Anregung: Jo Niemeyer, Berlin
1 Worum geht es?
Es wird eine Methode besprochen, einen Winkel in eine ungerade Anzahl gleicher Teile zu unterteilen.
2 Mit Zirkel und Lineal
Die Winkeldrittelung ist — zusammen mit der Wrfelverdoppelung und der Quadratur des Kreises — eines der drei klassischen Probleme, die mit Zirkel und Lineal nicht lsbar sind.
Wie steht es mit der Winkelfnfteilung?
Und gleich noch eine Fangfrage: Kann ein Winkel mit Zirkel und Lineal in 17 gleiche Teile geteilt werden? – Nun hat doch Gau§ gezeigt, wie mit Zirkel und Lineal ein regelm§iges 17-Eck konstruiert werden kann. Daraus folgt allerdings noch nicht, dass ein beliebiger Winkel in 17 gleiche Teile geteilt werden kann. (Nach derselben Logik wre eine Winkeldrittelung mglich, da ein regelm§iges Dreieck mit Zirkel und Lineal konstruiert werden kann.) – Angenommen, ein beliebiger Winkel kann mit Zirkel und Lineal in 17 gleiche Teile geteilt werden. Dann knnen wir insbesondere die Sektorenwinkel des regelm§igen 17-Ecks mit Zirkel und Lineal in je 17 gleiche Teile unterteilen und erhielten so das regelm§ige 172-Eck, also das regelm§ige 289-Eck. Dies widerspricht einem Satz von Gau§. Die Konstruktionsbedingung ist, dass die Eckenzahl sich aus verschiedenen FermatÕschen Primzahlen und/oder Zweierpotenzen zusammensetzt. Quadrate von FermatÕschen Prinzahlen sind als Eckenzahlen ausgeschlossen.
Allgemein kann ein Winkel nicht in eine ungerade Zahl von gleichen Teilen geteilt werden. Wenn dies mglich wre, konnten wir insbesondere den vollen Winkel unterteilen und erhielten ein regelm§iges Vieleck. Die Zahl msste dann eine FermatÕsche Primzahl sein. Weitere Unterteilung mit derselben Zahl fhrt zum analogen Widerspruch wie oben.
Wir knnen einen beliebigen Winkel mit Zirkel und Lineal nur unterteilen in Anzahlen gleicher Teile, die keine ungeraden Zahlen als Faktoren enthalten. Die Anzahlen mssen also reine Zweierpotenzen sein.
3 Winkeldrittelung
Es gibt verschiedene Methoden zur Winkeldrittelung, vgl. [1], [2], [3].
3.1 Konstruktion einer Kurve
Wir
arbeiten mit folgender Kurve: Auf der positiven x-Achse whlen wir den Punkt ![]() mit
mit ![]() (Abb. 1a). Weiter sei A der Koordinatenursprung. Wir ergnzen
die Punkte A und B zum rechtwinkligen Dreieck ABC
mit der Kathete a = 1. Anschlie§end
spiegeln wir das Dreieck ABC an der
Kathete AC zum Bilddreieck ACD. Unsere Kurve ist nun die Ortslinie
von D bei Variation von t (Abb. 1b).
(Abb. 1a). Weiter sei A der Koordinatenursprung. Wir ergnzen
die Punkte A und B zum rechtwinkligen Dreieck ABC
mit der Kathete a = 1. Anschlie§end
spiegeln wir das Dreieck ABC an der
Kathete AC zum Bilddreieck ACD. Unsere Kurve ist nun die Ortslinie
von D bei Variation von t (Abb. 1b).
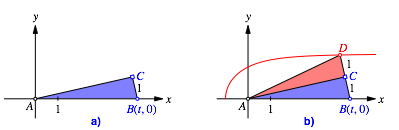
Abb. 1: Konstruktion der Kurve
3.2 Anwendung der Kurve zur Winkeldrittelung
Wir passen den zu drittelnden Winkel so ein, dass A der Scheitel ist, die positive x-Achse der eine Schenkel, und der andere Schenkel nach oben schaut (Abb. 2a).
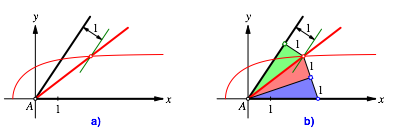
Abb. 2: Winkeldrittelung
Zu diesem zweiten Schenkel zeichnen wir eine Parallele im Abstand 1 und schneiden diese mit unserer Kurve (Abb. 2a). Der Strahl von A durch den Schnittpunkt drittelt den gegebenen Winkel. Die Abbildung 2b liefert den Beweis.
3.3 Rechnerisches
Fr den
Winkel ![]() im rechtwinkligen Dreieck ABC der Abbildung 1 gilt:
im rechtwinkligen Dreieck ABC der Abbildung 1 gilt:
![]() (1)
(1)
Der Punkt
D hat den Polarabstand t vom Ursprung und den Polarwinkel ![]() .
Fr seine kartesischen Koordinaten gilt daher:
.
Fr seine kartesischen Koordinaten gilt daher:
![]() (2)
(2)
Weiter ist:
![]() (3)
(3)
Aus (2) erhalten wir durch Expandieren (flei§iges Anwenden der Additionstheoreme):
![]() (4)
(4)
Damit haben wir eine Parameterdarstellung unserer Kurve.
Den Parameter t knnen wir eliminieren wie folgt. Zunchst folgt aus (4) durch Quadrieren:
![]() (5)
(5)
Vorsicht: Durch das Quadrieren knnen ãfalsche LsungenÒ entstehen.
Nun knnen wir (3) in (5) einsetzen. Die entstehende implizite Gleichung in x und y kann umgeformt werden zu:
![]() (6)
(6)
Die Abbildung 3 zeigt den Implicitplot von (6). Die Kurve der Abbildung 1 ist zustzlich an den Achsen gespiegelt. Das sind die ãfalschen LsungenÒ.
ber geometrische Aspekte dieser Kurve siehe [3].
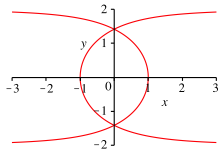
Abb. 3: Implicitplot der Kurve fr die Winkeldrittelung
4 Winkelfnfteilung
Die Winkelfnfteilung luft analog zur Winkeldrittelung.
Die Abbildung 4 zeigt die Konstruktion der Kurve fr die Winkelfnfteilung.
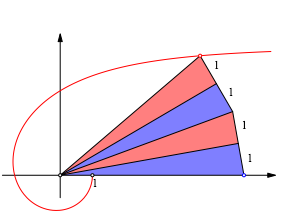
Abb. 4: Kurve fr die Winkelfnfteilung
Die Abbildung 5 zeigt das Vorgehen der Winkelfnfteilung.

Abb. 5: Winkelfnfteilung
Der Beweis luft analog.
Fr die Kurve erhalten wir die Parameterdarstellung:
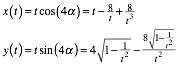 (7)
(7)
Elimination von t gem§ (2) fhrt auf die implizite Gleichung:
![]() (8)
(8)
Die Abbildung 6 zeigt den zugehrigen Implicitplot.
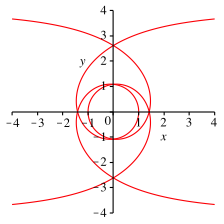
Abb. 6: Implicitplot fr die Winkelfnfteilung
5 Winkelsiebenteilung
Fr die Kurve fr die Winkelsiebenteilung erhalten wir die Parameterdarstellung:
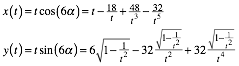 (9)
(9)
Die Abbildung 7 zeigt die Kurve.
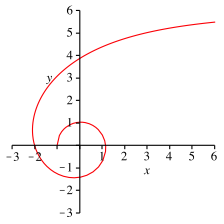
Abb. 7: Kurve fr die Siebenteilung
Elimination von t aus (9) fhrt zur impliziten Gleichung:
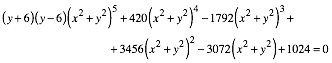 (10)
(10)
Die Abbildung 8 zeigt den zugehrigen Implicitplot.
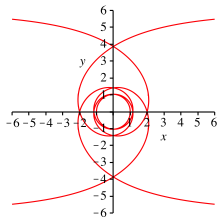
Abb. 8: Implicitplot fr die Siebenteilung
6 Winkelneunteilung
Ich wei§, es bastanzt nachgerade, aber ich sehe immer noch nicht durch.
Fr die Kurve fr die Winkelneunteilung erhalten wir die Parameterdarstellung:
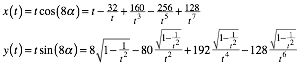 (11)
(11)
Die Abbildung 9 zeigt die Kurve.
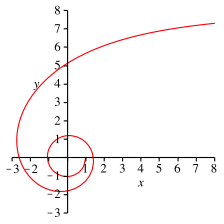
Abb. 9: Kurve fr die Neunteilung
Elimination von t aus (11) fhrt zur impliziten Gleichung:
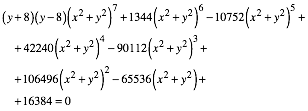 (12)
(12)
Die Abbildung 10 zeigt den zugehrigen Implicitplot.
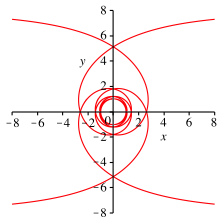
Abb. 10: Implicitplot fr die Neunteilung
7 Zusammenstellung und bersicht
Es werden jeweils der Reihe nach die Formeln fr Drittelung, Fnfteilung, Siebenteilung und Neunteilung notiert.
Bei den Koeffizientenschematas sind gewissen Gesetzm§igkeiten feststellbar, geschlossene Formeln habe ich nicht.
7.1 Parameterdarstellungen
Parameterdarstellung fr x(t):
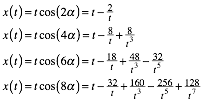 (13)
(13)
Koeffizientenschema mit Zeilensummen:
1
-2
-1
1
-8 8 1
1
-18 48 -32 -1
1
-32 160 -256 128
1
Parameterdarstellung fr y(t):
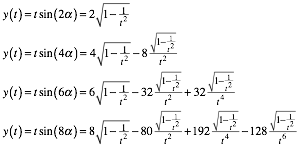 (14)
(14)
Koeffizientenschema mit Zeilensummen:
2
2
4
-8 -4
6
-32 32 6
8
-80 192 -128 -8
7.2 Implizite Gleichungen
Es wird das Koeffizientenschema angegeben:
 (15)
(15)
Man ist versucht, zwischen den Zeilen zu fllen. Wie geht das?
7.3 Kurven
Die Abbildung 11 zeigt die zugehrigen Kurven.
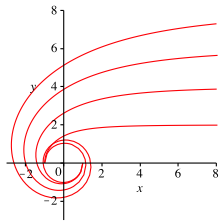
Abb. 11: Kurven
Die Abbildung 12 zeigt Kurven fr die Drittelung bis zur 17-Teilung.
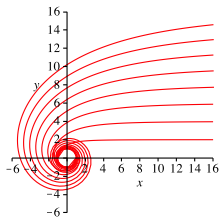
Abb. 12: Bis zur 17-Teilung
Websites
[1] Hans Walser: Winkeldrittelung (Abgerufen 07.08.2018):
www.walser-h-m.ch/hans/Miniaturen/W/Winkeldrittelung2/Winkeldrittelung2.htm
[2] Hans Walser: Winkeldrittelung (Abgerufen 02.08.2018):
www.walser-h-m.ch/hans/Miniaturen/W/Winkeldrittelung/Winkeldrittelung.htm
[3] Hans Walser: Winkeldrittelung (Abgerufen 14.08.2018):
www.walser-h-m.ch/hans/Miniaturen/W/Winkeldrittelung3/Winkeldrittelung3.htm