Hans Walser, [20190712]
Winkelverscherung
Anregung: Gerhard Stettler, Langnau
1 Worum geht es?
Bewegliche und rigide geometrische Figuren aus Metallwinkel. Rigide Modelle gibt es nur fr vier oder sechs Metallwinkel.
2 Das Holzmodell
Von Gerhard Stettler erhielt ich das Holzmodell der Abbildung 1.

Abb. 1: Holzmodell
Das
Holzmodell (es dient als Untersatz fr einen auf einer Ecke stehenden Wrfel) besteht
aus sechs halben Wrfeln. Die Wrfel sind lngs einer Diagonalebene halbiert,
es sind also Prismen mit einem rechtwinklig-gleichschenkligen Dreieck als
Grundflche. Die halben Quadrate sind kreuzweise an ihren Quadratseiten
verleimt. Die Oberflche des Holzmodells besteht aus sechs Rechtecken im
Seitenverhltnis ![]() (DIN-Format) und zwlf rechtwinklig-gleichschenkligen
Dreiecken.
(DIN-Format) und zwlf rechtwinklig-gleichschenkligen
Dreiecken.
3 Winkel und Scherengelenk
Wir denken uns die halben Wrfel nicht verleimt, sondern mit einem Pivot (drehbarer Stift) in den Quadratmitten verbunden. Damit funktionieren sie gleich wie Metallwinkel (Abb. 2a), welche durch eine (lockere) Schraube nach dem Prinzip eines Scherengelenks verbunden sind (Abb. 2b). Die Metallwinkel berhren sich auf der Au§enseite.


Abb. 2: Winkel und Scherengelenk
Technisches: Metallwinkel aus Stahlband, 16mm breit. Schenkellnge bis zur Bohrung 32mm. Bohrung 4.2mm. Gelenke aus M4-Schrauben, 8mm lang. Zwischen den Winkeln eine Unterlagscheibe.
4 Das Beispiel
Dem Holzmodell der Abbildung 1 entspricht das aus sechs Metallwinkeln gebaute Modell der Abbildung 3. Die Verscherungswinkel sind alternierend ±90¡.

Abb. 3: Sechs Metallwinkel
Das Modell ist rigide. Auch wenn die Schrauben noch nicht ganz angezogen sind, lsst es sich nicht mehr verscheren.
Die Achsenrichtungen der sechs Schrauben entsprechen den Richtungen der roten Kanten des Wrfelmodells der Abbildung 4.

Abb. 4: Schraubenrichtungen
Im Modell der Abbildung 5 sind die Schraubenrichtungen als Metallachsen realisiert.

Abb. 5: Achsen der Schraubenrichtungen
Es gibt (Abb. 7, 8, 10, 11) auch aus sechs Metallwinkeln gebaute flexible Modelle.
5 bersicht
Wir versuchen eine bersicht bezglich der Anzahl n der verbauten Metallwinkel. Die Kette der Metallwinkel soll geschlossen sein.
5.1 Keine Lsung mit zwei oder drei Metallwinkeln
Fr n = 2 und n = 3 habe ich keine Lsung gefunden.
5.2 Rigide Lsung mit vier Metallwinkeln
Fr n = 4 gibt es nur das rigide Modell der Abbildung 6. Das Modell ist flach. Die Verscherungswinkel sind 0¡.

Abb. 6: Vier Metallwinkel
5.3 Keine Lsung mit fnf Metallwinkeln
Fr n = 5 gibt es keine Lsung.
5.4 Zwei wesentlich verschiedene Lsungen mit sechs Metallwinkeln
Fr n = 6 gibt es zunchst die rigide Lsung der Abbildungen 3 und 5.
Wenn wir in diesem Modell eine Schraube lsen und das Modell andersherum wieder zusammenschrauben, ergibt es eine flexible Lsung. Die Abbildungen 7 und 8 zeigen zwei Situationen, welche ihrerseits ohne ffnen einer Schrauben ineinander bergefhrt werden knnen.

Abb. 7: Sechs Metallwinkel
In der Situation der Abbildung 8 sind die Verscherungswinkel ±90¡ oder 0¡.

Abb. 8: Andere Position
Die Achsenrichtungen der sechs Schrauben in der Abbildung 8 entsprechen den Richtungen der roten Kanten des Wrfelmodells der Abbildung 9.
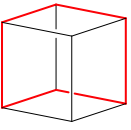
Abb. 9: Schraubenrichtungen
Im Modell der Abbildung 10 sind die Schraubenrichtungen als Metallachsen realisiert.

Abb. 10: Schraubenrichtungen als Achsen.
Das Modell ist flexibel (Abb. 11).

Abb. 11: Flexibles Modell
Im Prinzip handelt es sich hier um die vielerorts besprochene geometrische Knetmaschine.
5.5 Sieben Metallwinkel
Fr n = 7 gibt es zwei flexible Lsungen, die aber nicht ineinander berfhrbar sind.
Die Abbildungen 12, 13, 14, 15 zeigen zwei Situationen fr die eine Lsung.

Abb. 12: Sieben Metallwinkel. Erste Lsung. Bilaterale Symmetrie
Im Modell der Abbildung 13 sind die Schraubenrichtungen als Metallachsen realisiert.

Abb. 13: Schraubenrichtungen als Achsen
Die Abbildungen 14 und 15 zeigen eine andere Position. Diese ha keine Symmetrien.

Abb. 14: Sieben Metallwinkel. Erste Lsung, andere Position. Ohne Symmetrie
Das funktioniert auch mit Achsen (Abb. 15).

Abb. 15: Schraubenrichtungen als Achsen
Die Abbildungen 16 bis 19 zeigen zwei verschiedene Situationen fr die andere Lsung, Zunchst mit Schrauben, dann mit Achsen.

Abb. 16: Sieben Metallwinkel. Zweite Lsung. Bilaterale Symmetrie

Abb. 17: Schraubenrichtungen als Achsen

Abb. 18: Sieben Metallwinkel. Zweite Lsung, andere Position. Ohne Symmetrie

Abb. 19: Schraubenrichtungen als Achsen
5.6 Vermutung
Ich vermute, dass es fr n > 7 kein rigides Modell gibt, aber immer ein flexibles Modell. Es gibt bis auf Verscherungen genau ein Modell.
5.7 Acht Metallwinkel
Die Abbildungen 20 bis 2415 zeigen verschiedene Positionen fr das Modell mit acht Metallwinkeln.
In der Abbildung 20 haben wir eine vierteilige Rotationssymmetrie sowie eine Drehspiegelsymmetrie. Die Verscherungswinkel sind alternierend ±114.4698005¡.

Abb. 20: Acht Metallwinkel. Hohe Symmetrie
Die Situation der Abbildung 21 ist flach. Die Verscherungswinkel sind entweder 0¡ oder 180¡.

Abb. 21: Flache Situation
In der Situation der Abbildung 22 haben wir eine zweiteilige Drehsymmetrie sowie eine Drehspiegelsymmetrie.

Abb. 22: Recht spezielle Situation
In der Situation der Abbildung 23 sind die Verscherungswinkel 0¡, ±90¡, 180¡.

Abb. 23: Eine andere spezielle Situation
Die Abbildung 24 zeigt eine Verscherung (Parallelogramm) der Situation der Abbildung 23.

Abb. 24: Verscherung der Situation der Abb. 23
5.8 Zehn Metallwinkel
Die Abbildungen 25 bis 28 zeigen Situationen fr das Modell mit zehn Metallwinkeln.
Die Situation der Abbildung 25 hat eine hohe Symmetrie. Wir haben eine fnfteilige Drehsymmetrie sowie eine Drehspiegelsymmetrie. Die Verscherungswinkel sind alternierend ±128.1727076¡.

Abb. 25: Hohe Symmetrie
In den Situationen der Abbildungen 26, 27 und 26 haben wir nur Verscherungswinkel von 0¡, ±90¡ und 180¡.

Abb. 26: Spezielle Verscherungswinkel

Abb. 27: Spezielle Verscherungswinkel

Abb. 28: Spezielle Verscherungswinkel
6 Drehsymmetrie
Die Beispiele der Abbildungen 5, 3, 11 und 16 haben dieselbe Symmetriestruktur. Wir haben eine Drehsymmetrie und eine Drehspiegelsymmetrie. Die Verscherungswinkel sind alternierend und betragsm§ig konstant. Die Anzahl der Metallwinkel ist gerade.
Die Tabelle 1 gibt die Verscherungswinkel fr die ersten Beispiele.
|
Anzahl Metallwinkel |
Verscherungswinkel |
|
4 |
0¡ |
|
6 |
90¡ |
|
8 |
114.4698005¡ |
|
10 |
128.1727076¡ |
|
12 |
137.0585971¡ |
|
14 |
143.3155429¡ |
|
16 |
147.9687631¡ |
|
18 |
151.5682942¡ |
|
20 |
154.4372211¡ |
|
22 |
156.7782817¡ |
|
24 |
158.7253182¡ |
|
100 |
174.9079930¡ |
|
10000 |
179.9490882¡ |
Tab. 1: Verscherungswinkel im symmetrischen Fall
Der Verscherungswinkel w berechnet sich in diesem symmetrischen Fall mit:
![]() (1)
(1)
7 Link mit gleichseitig-rechtwinkligen Polygonen
Die Schraubenachsen unserer Modelle bilden ein geschlossenes n-seitiges gleichseitig-rechtwinkliges Polygon. Die Seitenlnge ist das Doppelte der Schenkellnge der Metallwinkel. Die Rechtwinkligkeit ergibt sich daraus, dass die Metallwinkel einen rechten Winkel einschlie§en.
Die Verscherungswinkel entsprechen den Torsionen der Kanten des gleichseitig-rechtwinkligen Polygons.
8 Ausblick
Wir haben unter ãWinkelÒ stillschweigend rechte Winkel verstanden. Wie ist es mit Metallwinkeln, die einen anderen Winkel einschlie§en?
Websites
Hans Walser: Gleichseitig-rechtwinklige Polygone im Raum
http://www.walser-h-m.ch/hans/Miniaturen/G/Gls_rw_Polygone/Gls_rw_Polygone.htm
Hans Walser: Siebeneck im Raum
http://www.walser-h-m.ch/hans/Miniaturen/S/Siebeneck/Siebeneck.htm