Hans Walser, [20161011]
Winkler-Graph
1 Worum geht es?
Es wird eine Schritt-fŸr-Schritt-Konstruktion des Winkler-Graphs (Winkler 2016) mit Beweis der Schlie§ungseigenschaft besprochen.
Der Winkler-Graph (Abb. 1) ist ein 4-regulŠrer Streichholzgraph mit 114 Kanten. Nach dem Harborth-Graph (104 Kanten) ist er der zweitkleinste bekannte 4-regulŠre Streichholzgraph.
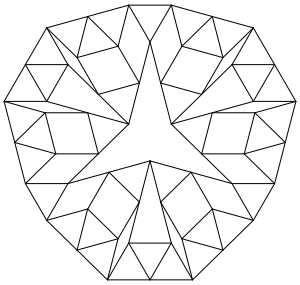
Abb. 1: Winkler-Graph
2 Konstruktionsvorgang
Wir beginnen mit drei gleichseitigen Dreiecken der KantenlŠnge 1 gemŠ§ Abbildung 2.
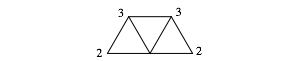
Abb. 2: Beginn
Bei den noch nicht regulŠren Knoten ist die Anzahl der einmŸndenden Kanten angegeben.
Nun bauen wir ein gleichschenkliges Dreieck der SchenkellŠnge 2 auf (Abb. 3).
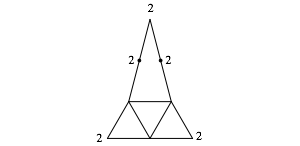
Abb. 3: Gleichschenkliges Dreieck
Wir ergŠnzen gemŠ§ Abbildung 4 mit zwei Dreiecken und zwei Rhomben.
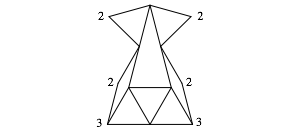
Abb. 4: Dreieck und Rhombus
Wir fŸgen zwei weitere Rhomben an (Abb. 5).
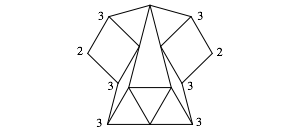
Abb. 5: Rhombus
Der obere der beiden in der Abbildung 6 rot eingezeichneten Winkel ist Au§enwinkel des gleichseitigen Dreiecks und misst 120¡. Der untere Winkel hat parallele Schenkel und ist daher gleich gro§.
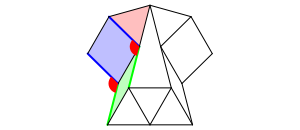
Abb. 6: Winkel von 120¡
Wir kšnnen also gleichseitige Dreiecke einfŸgen (Abb. 7).
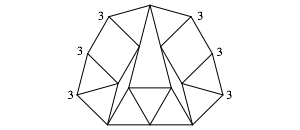
Abb. 7: Gleichseitige Dreiecke
3 Triplet-Kite
Nun kšnnen wir mit gleichseitigen Dreiecken und Rhomben zum Triplet-Kite erweitern (Abb. 8).
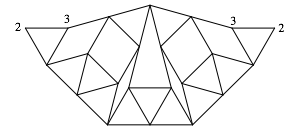
Abb. 8: Triplet-Kite
Die beiden FlŸgeldreiecke im Triplet-Kite sind seitenparallel. Das geht aus der RichtungsŸbertragungskette der Abbildung 9 hervor.
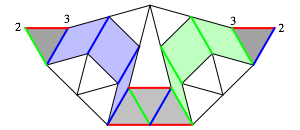
Abb. 9: RichtungsŸbertragung
In der Abbildung 10 sind drei um 120¡ verdrehte Triplet-Kites eingezeichnet. Deren FlŸgeldreiecke sind seitenparallel und kšnnen daher Ÿberlagert und identifiziert werden. So erhalten wir den Winkler-Graphen der Abbildung 1.
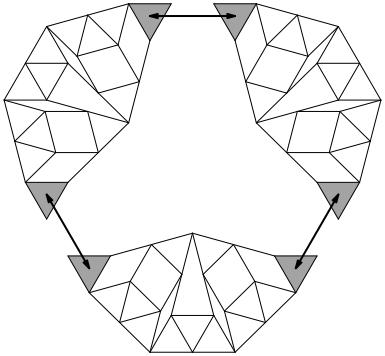
Abb. 10: Drei Triplet-Kites
4 RegularitŠt
Die Abbildung 11 illustriert die Anzahlen der einmŸndenden Kanten. Der Gesamtgraph ist regulŠr.
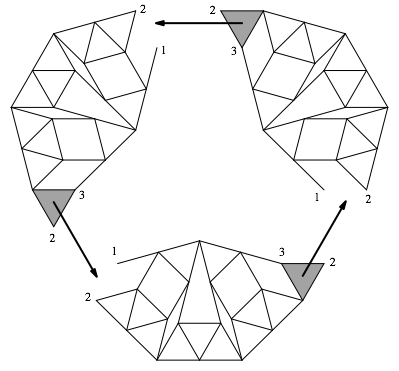
Abb. 11: RegulŠrer Graph
5 Schlie§ungsfigur
In der Abbildung 1 ist die RichtungsŸbertragung als Schlie§ungsfigur dargestellt.
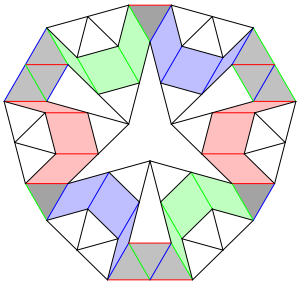
Abb. 12: RichtungsŸbertragung
Literatur
Winkler, Mike (2016): Ein neuer 4-regulŠrer Streichholzgraph. Mitteilungen der DMV 24 / 2016. 74-75.
Winkler, Mike und Dinkelacker, Peter und Vogel, Stefan (2016): New minimal (4,n)-regular matchstick graphs. arXiv:1604.07134v2
Links
Harborth-Graph (09.10.2016):
https://de.wikipedia.org/wiki/Streichholzgraph#/media/File:Harborth_graph_vector.svg
Mike Winkler Homepage (09.10.2016):