Hans Walser, [20190306]
WŸrfel-Tribar
Anregung: B. W., K.
1 Worum geht es?
Ein aus WŸrfeln gebautes Tribar (Abb. 1) fŸhrt zu Fragen des Passens und Einpassens.
Abb. 1: WŸrfel-Tribar
2 Passen und Einpassen
Wir denken uns die neun gelben WŸrfel der Abbildung 1 fest verleimt.
Kann ein zehnter WŸrfel (rot in Abb. 2) eingefŸgt werden?
Abb. 2: Passt der rote WŸrfel?
Der rote WŸrfel passt in die LŸcke (statisches Passen). Allerdings kann er nicht von au§en in den Rahmen der Abbildung 1 eingefŸgt werden (kinematisches Einpassen). Und aus der Situation der Abbildung 2 kann er nicht ohne Zerstšrung des gelben Rahmens entfernt werden.
3 Borromei-WŸrfel
Die Abbildung 3 zeigt das nŠchstgrš§ere WŸrfel-Tribar. Die gelben WŸrfel seien wiederum fest verleimt.
Abb. 3: NŠchstgrš§eres Tribar
Der rote, der blaue und der grŸne WŸrfel (Abb. 4) seinen einzeln und lose.
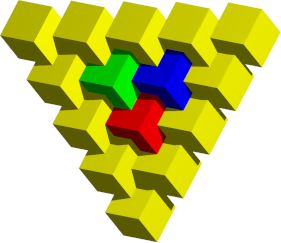
Abb. 4: Borromei-WŸrfel
Es ist nicht mšglich, diese drei losen WŸrfel aus dem gelben Rahmen zu entfernen. Sobald aber einer der drei WŸrfel durch Zerstšren (zum Beispiel Wegspitzen oder Ausbohren) entfernt ist, kšnnen die beiden anderen problemlos herausgeschoben werden.
Jeder der drei losen WŸrfel verhindert ein Herausfallen der beiden anderen.
Wir haben also eine analoge Situation wie bei den drei Borromeischen Ringen, allerdings nicht aus topologischen sondern aus geometrischen GrŸnden.