Hans Walser, [20170827a]
WŸrfel auf Ecke
Anregung und Idee: B. K., Z.
1 Worum geht es?
Wie wahrscheinlich ist es, dass ein SpielwŸrfel auf einer Ecke stehenbleibt (Abb. 1)?
Abb. 1: WŸrfel auf Ecke
Der Autor gesteht, dass er den WŸrfel sehr sorgfŠltig so hingestellt hat.
2 Analyse des SpielwŸrfels
Ein SpielwŸrfel ist nicht einfach ein regelmŠ§iges Hexaeder (Kubus, WŸrfel im geometrischen Sinn) mit allenfalls leicht abgerundeten Ecken und Kanten. Das ãAbrundenÒ der Ecken geschieht systematisch wie folgt.
Wir beginnen mit einem regelmŠ§igen Hexaeder zusammen mit seiner Kantenmittenkugel (Abb. 2a). Die Kantenmittenkugel berŸhrt, wie der Name sagt, die Kantenmitten des Hexaeders. Sie liegt also zwischen der Inkugel und der Umkugel des Hexaeders.
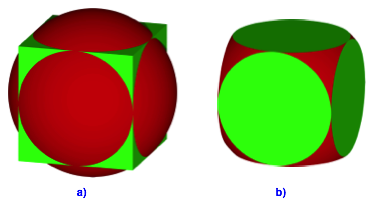
Abb. 2: Hexaeder mit Kantenmittenkugel
Der SpielwŸrfel ist nun geometrisch die Schnittfigur des Hexaeders mit seiner Kantenmittenkugel (Abb. 2b).
Wenn nun der SpielwŸrfel sorgfŠltig auf einen inneren roten Punkt der OberflŠche in der Abbildung 2b auf eine horizontale Ebene abgelegt wird, befindet sich sein Schwerpunkt senkrecht oberhalb des Auflagepunktes. Der SpielwŸrfel bleibt stehen.
3 Was geschieht beim WŸrfeln?
Die Wšrter WŸrfel und wŸrfeln kommen von Wurf oder werfen. Beim WŸrfeln erhŠlt der SpielwŸrfel einen Impuls, der ihn, falls er auf einem roten Punkt auftrifft, weiterrollen lŠsst, bis er auf eine grŸne SeitenflŠche einschnappt.
4 Sprachliches
Eigentlich ist es falsch, ein regulŠres Hexaeder (Kubus) als ãWŸrfelÒ zu bezeichnen. Der SpielwŸrfel ist vielmehr eine Kugel mit sechs abgeschnittenen Kugelkalotten.
Die englischen Bezeichnungen sind differenziert: das Hexaeder (der Kubus) wird als cube bezeichnet, der SpielwŸrfel als dice.
5 Berechnungen
FŸr die
Berechnungen nehmen wir an, das regulŠre Hexaeder habe die KantenlŠnge 2. Die
Kantenmittenkugel hat damit den Radius 
und die
OberflŠche 
. Die sechs Kugelkalotten (Hauben) der Abbildung 2a
haben je die Hšhe 
und damit
den FlŠcheninhalt 
. Der Anteil der sechs KugelkalottenflŠchen an der OberflŠche
der Kantenmittenkugel ist daher:
(1)
Der FlŠchenanteil der acht roten Dreiecke der Abbildung 2b an der Kantenmittenkugel ist daher etwa 12.132%. Das ist auch die Wahrscheinlichkeit dafŸr, dass der SpielwŸrfel bei sorgfŠltigem, will sagen impulslosem Absetzen auf einen roten Punkt stehen bleibt.
6 Bemerkungen
Die acht roten Dreiecke der Abbildung 2b sind von Kleinkreisen begrenzt. Sie sind keine Eulersche sphŠrische Dreiecke, da diese von Gro§kreisen begrenzt sein mŸssen. Die berŸhmte FlŠchenformel mit dem sphŠrischen Exzess ist daher nicht anwendbar.
Die sechs
grŸnen KreisflŠchen der Abbildung 2b haben insgesamt einen FlŠcheninhalt 6¹.
Ihr FlŠchenverhŠltnis zur OberflŠche der Kantenmittenkugel ist daher 
. FŸr unsere †berlegungen ist das aber nicht relevant.