Hans Walser, [20111016b]

Würfel und Oktaeder

1 Oktaeder im Würfel

Welches ist das größte Oktaeder, das einem Würfel einbeschrieben werden kann? Wir beschreiben die Konstruktion in zwei Schritten.

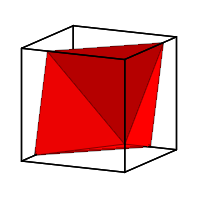
Zunächst nehmen wir die Seitenflächenmitten des Würfels als Eckpunkte des Oktaeders.

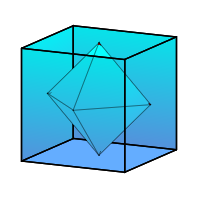
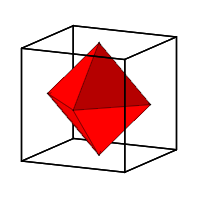
Oktaeder im Würfel

Das Volumen des Oktaeders ist des Würfelvolumens. Dieses Oktaeder ist das kleinste, das dem Würfel so einbeschreiben werden kann, dass jede Oktaederecke die Würfeloberfläche berührt.

Nun drehen wir das Oktaeder um eine Achse, welche einer Körperdiagonalen des Würfels entspricht, um 60°.

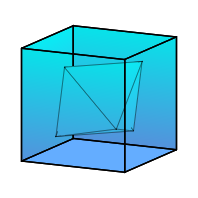
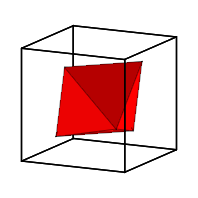
Gedrehtes Oktaeder

Anschließend strecken wir vom Zentrum aus mit dem Faktor . Natürlich hätte man Drehung und Streckung zu einer Drehstreckung zusammenfassen können.

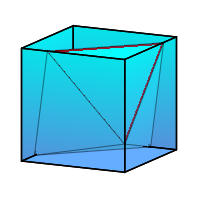
Gestreckt

Die Oktaederecken liegen auf Würfelkanten und vierteilen diese. Das Oktaeder ist vollständig verkeilt. Ich vermute, dass dies die optimale Lösung ist. Gegenüber dem ursprünglichen Oktaeder sind die Längen um den Faktor vergrößert worden. Das Volumen ist also mit dem Faktor vergrößert worden und beträgt nun des Würfelvolumens.

Es gibt insgesamt vier solcher Positionen für das Oktaeder, da es für die erste Drehung vier mögliche Körperdiagonalen als Achsen gibt.

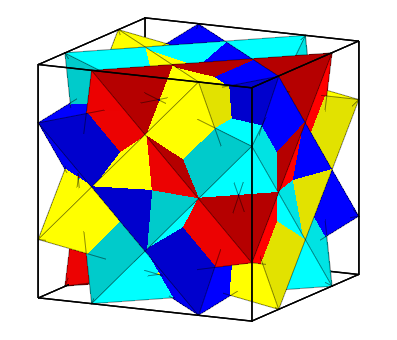
Vier Oktaeder im Würfel

Die Oktaederkanten auf der Würfeloberfläche dritteln sich gegenseitig.

Wenn wir den Würfel weglassen, ergibt sich ein Stern mit 24 Spitzen.

Stern

Die Schnittmenge der vier Oktaeder ist ein Kuboktaeder mit auf den Seitenquadraten aufgesetzten ziemlich flachen Pyramiden.

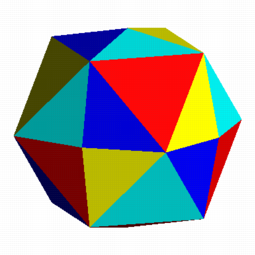
Durchdringung der vier Oktaeder

2 Würfel im Oktaeder

Welches ist der größte Würfel, der einem Oktaeder einbeschrieben werden kann? Wir beschreiben die Konstruktion in zwei Schritten.

Zunächst nehmen wir die Seitenflächenmitten des Oktaeders als Eckpunkte des Würfels. Das Volumen des so entstehenden Würfels ist des Oktaedervolumens.

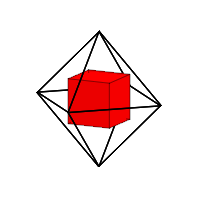
Würfel im Oktaeder

Nun drehen wir den Würfel um eine Körperdiagonale des Oktaeders (es gibt keine anderen Diagonalen im Oktaeder) um 45°.

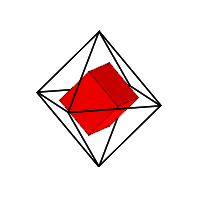
Gedrehter Würfel

Nun Strecken wir mit dem Faktor .

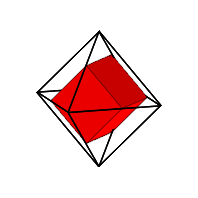
Gestreckter Würfel

Die Würfelecken teilen die Oktaederkanten im Verhältnis . Das ist das Verhältnis der Seiten eines Rechtecks im DIN-Format.

Das Volumen des Würfels ist nun des Oktaedervolumens.

Es gibt drei Positionen des Würfels im Oktaeder.

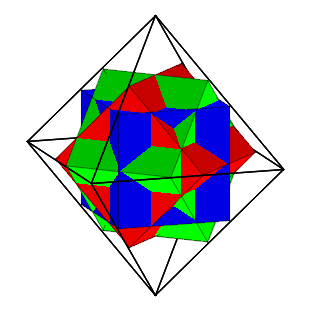
Drei Würfel im Oktaeder

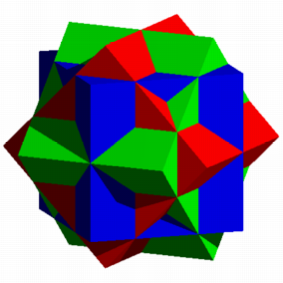
Würfelstern

Die Schnittmenge der drei Würfel ist ein an den Ecken bis auf die Inkugel herab abgestumpftes Rhombendodekaeder.

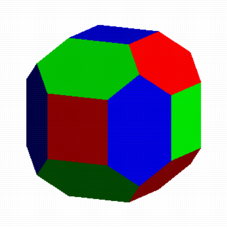
Durchdringung der drei Würfel

Wer Lust hat, kann das selbe Spielchen für Ikosaeder und Dodekaeder durchführen.