Hans Walser, [20170809]
Wrfel und Oktaeder
Anregung: H. Sch., W.
1 Worum geht es?
Das Kantenmittenviereck eines Quadrates ist wiederum ein Quadrat (Abb. 1a). Die Diagonalen des einbeschriebenen roten Quadrates sind parallel zu den Seiten des schwarzen Ausgangsquadrates.

Abb. 1: Quadrat im Quadrat
Wir knnen aber dem schwarzen Quadrat auch ein schiefstehendes rotes Quadrat einbeschreiben (Abb. 1b). Die Diagonalen des roten Quadrates sind nicht mehr parallel zu den Seiten des schwarzen Quadrates.
Im dreidimensionalen Raum bilden die Seitenmitten eines Wrfels die Eckpunkte eines Oktaeders (Abb. 2a). Kann dem Wrfel auch ein schiefstehendes regulres Oktaeder einbeschrieben werden?

Abb. 2: Oktaeder im Wrfel
2 Oktaederecken auf Wrfelkanten
Wir whlen im Wrfel zwei diametrale Eckpunkte (blau in Abb. 3a). Die drei von diesen Wrfelecken ausgehenden Kanten unterteilen wir im Verhltnis 3:1 (rot in Abb. 3a). Die insgesamt sechs Teilpunkte sind die Ecken eines regulren Oktaeders (Abb. 3b).
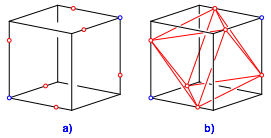
Abb. 3: Okteaderecken auf Wrfelkanten
Von den zwlf Oktaederkanten liegen sechs auf der Wrfeloberflche. Diese haben im Einheitswrfel die Lnge:
![]() (1)
(1)
Die anderen sechs Oktaederkanten verlaufen im Wrfelinneren. Fr ihre Lnge ergibt sich:
![]() (2)
(2)
Das Oktaeder ist also regulr. Zu diesem Beispiel siehe [1] .
3 Allgemeine Lsung
Wir legen ein Koordinatensystem so in den Wrfel, dass der Ursprung im Wrfelmittelpunkt liegt, die Koordinatenachsen parallel zu den Wrfelkanten liegen und die Seitenlnge des Wrfels 2 ist (Abb. 4).

Abb. 4: Koordinatensystem
Nun legen
wir einen Doppelkegel in den Wrfel. Der Doppelkegel hat die Spitze im
Ursprung, die Achse geht durch den Punkt ![]() und der
halbe
ffnungswinkel ist:
und der
halbe
ffnungswinkel ist:
![]() (3)
(3)
Die Abbildung 5 zeigt die Situation. Der Doppelkegel enthlt Tripel paarweise orthogonaler Mantellinien.
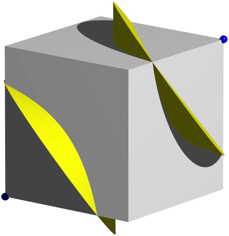
Abb. 5: Doppelkegel im Wrfel
Der Doppelkegel schneidet aus jeder Wrfelseite eine Hyperbel heraus. Fr das Deckquadrat des Wrfels (z = 1) hat die Hyperbel die Gleichung (CAS):
![]() (4)
(4)
Auf
dieser Hyperbel liegen also beispielsweise der Seitenmittelpunkt des Deckquadrates,
was zum Oktaeder der Abbildung 2a fhrt, oder der Punkt ![]() , was zum Oktaeder der Abbildung 3b fhrt.
, was zum Oktaeder der Abbildung 3b fhrt.
Wir knnen nun irgendeinen Punkt auf dieser Hyperbel whlen. Zusammen mit den entsprechenden Punkten auf den anderen Wrfelseiten erhalten wir die sechs Eckpunkte eines regulren Oktaeders.
Beispiel:
Der Punkt ![]() erfllt
(4). Die sechs Punkte (rot in Abb. 6a)
erfllt
(4). Die sechs Punkte (rot in Abb. 6a)
![]() (5)
(5)
sind die Ecken eines regulren Oktaeders. Man rechnet leicht nach, dass die Diagonalen alle gleich lang und paarweise orthogonal sind.
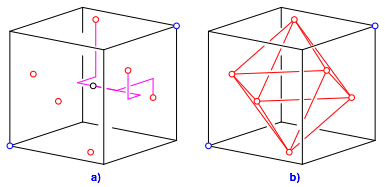
Abb. 6: Allgemeiner Fall
4 Volumenanteile
Das Volumen des Oktaeders der Abbildung 2a ist ein Sechstel des Wrfelvolumens.
Das
Volumen des Oktaeders der Abbildung 3b ist ![]() des Wrfelvolumens.
des Wrfelvolumens.
Das
Volumen des Oktaeders der Abbildung 6b ist ![]() des
Wrfelvolumens.
des
Wrfelvolumens.
Websites
[1] Hans Walser: Wrfel und Oktaeder (10.08.2017):
www.walser-h-m.ch/hans/Miniaturen/W/Wuerfel_und_Oktaeder/Wuerfel_und_Oktaeder.htm