Hans Walser, [20080320a]
WŸrfeldurchdringung
Prinz Rupert (1619-1682) zeigte: Durch einen WŸrfel kann ein derart gro§es Loch mit quadratischem Querschnitt gestanzt werden, dass ein zweiter gleich gro§er WŸrfel hindurch geschoben werden kann.
In der Figur ist links der WŸrfel in Grund- und Aufriss gezeichnet. Eine Kšrperdiagonale ist erstprojizierend. Dem roten Seitenquadrat gegenŸber liegt ein grŸnes Seitenquadrat, dem blauen gegenŸber ein oranges und dem gelben gegenŸber ein violettes.
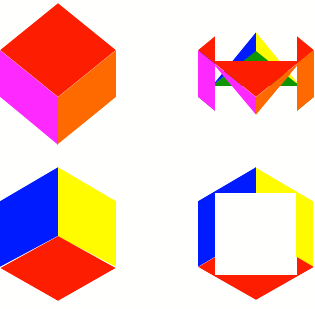
Das quadratische Loch
durch den WŸrfel
Rechts der WŸrfel mit
einem Loch. Die Lochachse ist koaxial zur erstprojizierenden WŸrfeldiagonalen.
Die Lochseiten sind parallel zu Auf- und Seitenrissebene. Der quadratische
Querschnitt ist gerade gro§ genug, um einen zweiten WŸrfel hindurch zuschieben.
Der Witz der Sache ist,
dass im Grundriss das quadratische Loch (knapp) innerhalb des WŸrfelumrisses
verlŠuft.
Um dieses einzusehen,
arbeiten wir rein planimetrisch im Grundriss mit dem in der folgenden Figur
angegebenen Koordinatensystem (beachte die Richtung der x-Achse, aber das ist in der darstellenden Geometrie
so Ÿblich). Wir wŠhlen die WŸrfelkante gleich eins. Damit hat die Lochecke unten rechts die Koordinaten 
.
Da der Grundriss eine
isometrische Normalaxonometrie ist, ergibt sich das VerkŸrzungsverhŠltnis 
. Wegen 
(das ist eine Formel
aus der Theorie der Normalaxonometrie) folgt 
. Dies ist die SeitenlŠnge und auch der Umkreisradius des
regelmŠ§igen Sechseckes, welches als WŸrfelumriss erscheint. FŸr die
eingezeichnete Konturlinie erhalten wir die Gleichung 
. Einsetzen der Eckpunktskoordinaten 
liefert 
. Die Ecke liegt also knapp oberhalb der Konturlinie.
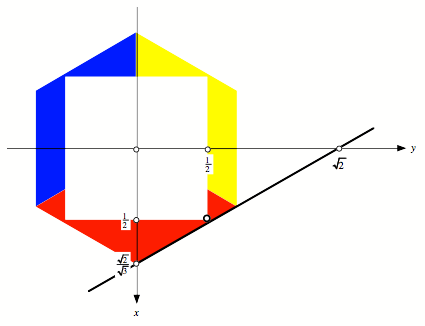
Im Grundriss
Die folgenden Bilder
zeigen zunŠchst eine Ansicht des ursprŸnglichen (roten) WŸrfels und desselben
WŸrfels in gelochtem Zustand.
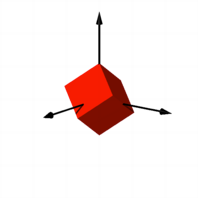
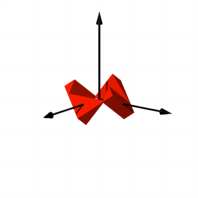
WŸrfel und gelochter
WŸrfel
Und nun fahren wir
einen kongruenten (grŸnen) WŸrfel durch.
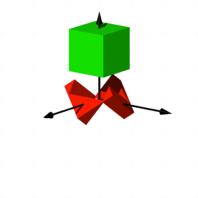
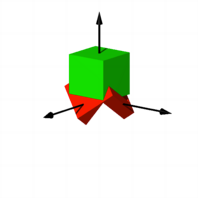
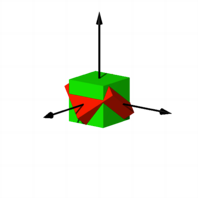
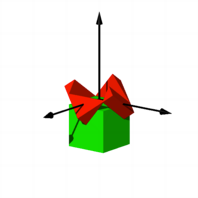
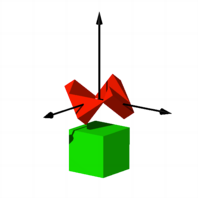
Der grŸne WŸrfel
durchdringt den roten WŸrfel
Literatur
[Jerrard/Wetzel 2008] Jerrard, Richard P. and John E. Wetzel: Universal Stoppers Are Rupert. The College Mathematics Journal. Vol. 39, No. 2, March 2008