Hans Walser, [20130510a]
Wrfelecke und Davidstern
Anregung: A. W., L.
1 Die Wrfelecke
Eine Wrfelecke, also einen rumlichen rechten Winkel, knnen wir aus drei rechtwinklig gleichschenkligen Dreiecken bauen, deren Katheten wir aneinanderfgen (Abb. 1).
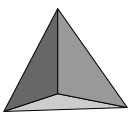
Abb. 1: Rumliche Ecke
Aus einem quadratischen Papier (Origami Papier) knnen wir eine solche Wrfelecke basteln wie folgt: Wir falten die beiden Diagonalen und schneiden eine Diagonale bis zur Mitte ein. Die beiden an den Schnitt anschlie§enden Dreiecke sind zu identifizieren, also zum Beispiel zu verkleben oder mit Staplerklammern oder Broklammern zu verheften. Alternativ knnen wir auch die beiden Dreiecke komplementr mit Schlitzen versehen und dann ãeinhngenÒ. Wir brauchen dann keine Bindemittel.
Die Abbildung 2 zeigt das Falt- und Schnittmuster.
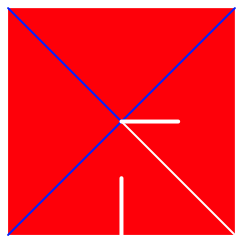
Abb. 2: Falt- und Schnittmuster
Das ãEinhngenÒ soll so geschehen, dass die losen Ecken ins Innere zu liegen kommen.
2 Die Pyramide
Die Abbildung 3 zeigt das Modell von innen und von au§en.


Abb. 3: Modell von innen und von au§en
Wir knnen das Modell auch als eine Dreikant-Pyramide mit einem gleichseitigen Dreieck als Basis interpretieren.
3 Der Stern
Die Idee ist nun, zwei solche Modelle um 60¡ verdreht anzuordnen. In der Grundflche entsteht dann ein Davidstern.
Fr die Durchdringung der beiden Pyramiden brauchen wir zustzliche Schlitze. Das Vorgehen ist folgendes. Wir falten die quadratischen Papiere vor dem ãEinhngenÒ so, dass je ein vierlagiges rechtwinklig gleichschenkliges Dreieck entsteht. Dann dritteln wir die Hypotenuse und bringen komplementre Schlitze an gem§ Abbildung 4.

Abb. 4: Komplementre Schlitze
Nun falten wir wieder auf, bauen durch Einhngen die beiden Pyramiden und durchdringen sie mit Hilfe der vorbereiteten Schlitze. Das braucht etwas Fingerspitzengefhl, ist aber machbar.
Die Abbildung 5 zeigt den rumlichen Stern von oben und von unten. Bei der Sicht von unten erkennen wir den Davidstern.


Abb. 5: Rumlicher Stern und Davidstern
4 Der Goldene Schnitt
Mit einigen Handgriffen finden wir auch den Goldenen Schnitt (Walser 2013). Es geht sogar auf zwei Arten. Dazu ergnzen wir die Figur der Abbildung 4 zur Figur der Abbildung 6. Der Major ist jeweils blau, der Minor rot eingezeichnet. Beweise durch Nachrechnen.
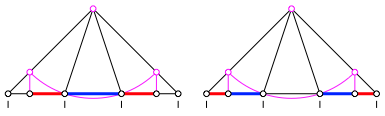
Abb. 6: Der Goldene Schnitt
Literatur
Walser, Hans (6. Auflage). (2013). Der Goldene Schnitt. Mit einem Beitrag von Hans Wu§ing ber populrwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.