1 Worum geht es?

Verallgemeinerung des Quadratfraktals in den Raum.

Schöne Bildchen

2 Quadratfraktal

2.1 Klassisch

Abb. 1: Erste Schritte

Abb. 2: Quadratfraktal

2.2 Als Baumfraktal

Genau genommen ist die Grenzsituation der Figuren der Abbildungen 1 und 2 kein Fraktal, da nirgends eine verkleinerte Kopie der Gesamtfigur als Teil vorkommt. Tatsächlich muss für Konstruktion und Verständnis modifiziert im Sinne eines Baumfraktals vorgegangen werden.

Das Startquadrat ist der Baumstamm. Und es sprießen schrittweise drei Äste heraus. Jeder Ast oder Teilast ist eine Kopie des ganzen Baumes.

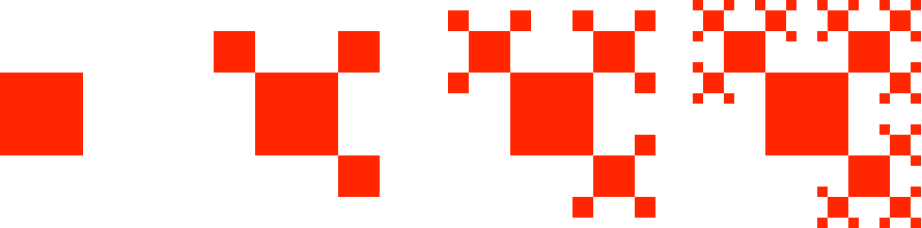
Abb. 3: Baumfraktal

Abb. 4: Wachstum des Baumes

Technisch wird zuerst ein Baum generiert, und am Schluss ein vierter Ast angehängt.

2.3 Mit Kreisen

Die Quadrate können durch andere Figuren ersetzt werden (Abb. 5).

Abb. 5: Inkreise und Umkreise der Quadrate

3 Würfelfraktal

Beim Würfelfraktal wird ebenfalls zunächst ein Baum generiert. Aus jedem Ast wachsen sieben weitere Verästelungen. Dies hat zur Folge, dass aus Speichergründen nur wenige Generationen dargestellt werden können.