Hans Walser, [20230529]

Wuerfelfraktal

Anregung: Name dem Autor bekannt

1 Worum geht es?

Fraktale Spielerei mit modifizierten Würfeln. Unsichtbarkeit.

2 Sierpiński-Tetraeder

Wir skalieren einen Würfel (erstes Bild in Abb. 1) mit dem Faktor 1/2 und ordnen vier Kopien an gemäß dem zweiten Bild in Abbildung 1. Wiederholung des Prozesses führt zum Sierpiński-Tetraeder.

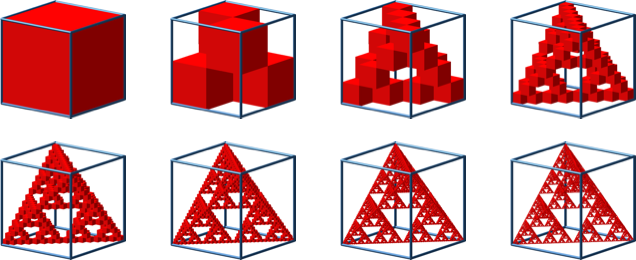
Abb. 1: Konstruktionsvorgang

Abb. 2: Dynamische Konstruktion

3 Modifikation des Würfels

Wir spannen in das Würfelgerüst zwei gleichseitige Dreiecke ein (Abb. 3).

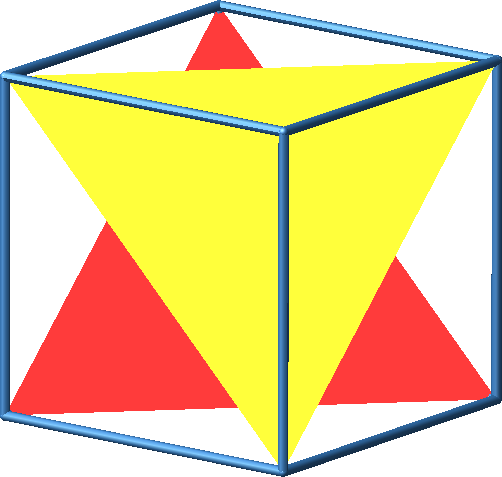
Abb. 3: Würfelgerüst mit gleichseitigen Dreiecken

Die Abbildungen 4 bis 6 zeigen verschiedene Ansichten. Es gibt Sichten, in denen man nichts sieht.

Abb. 4: Verschiedene Ansichten

In den Frontalansichten auf eine Würfelseite wird der Rahmen vollständig ausgefüllt (Abb. 5). Bei der Sicht über eine Würfelkante kann es vorkommen, dass man nichts sieht (Abb. 5, letztes Bild).

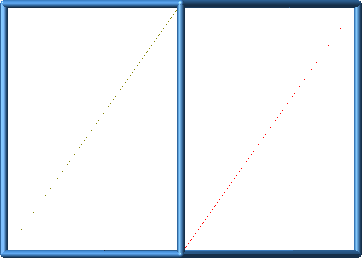
Abb. 5: Verschiedene Ansichten

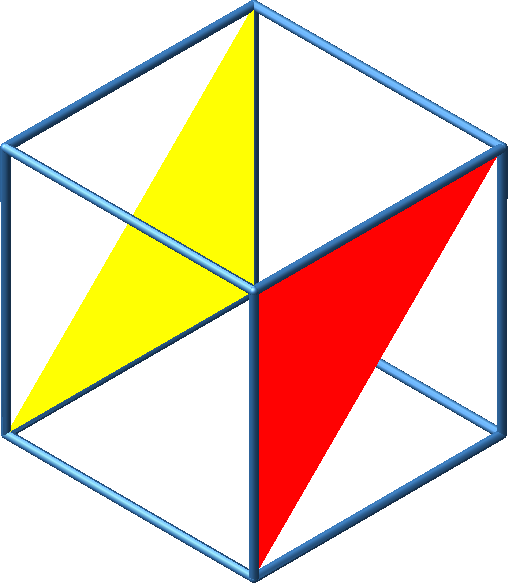
Abb. 6: Ansichten über Eck

4 Sierpiński-Tetraeder

Wir gehen gemäß Abbildung 1 vor (Abb. 7).

Abb. 7: Konstruktionsvorgang

Damit erhalten wir das in den Würfel eingepasste Sierpiński-Tetraeder (Abb. 8 bis 13).

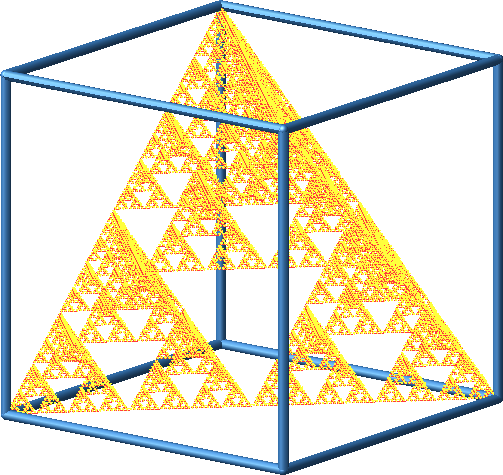
Abb. 8: Sierpiński-Tetraeder

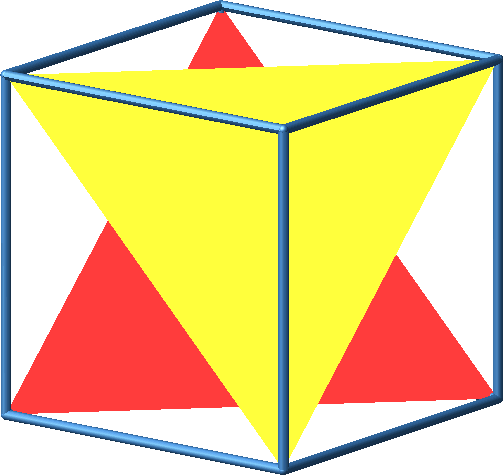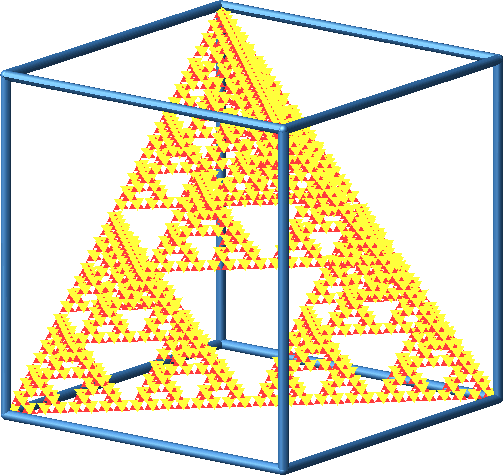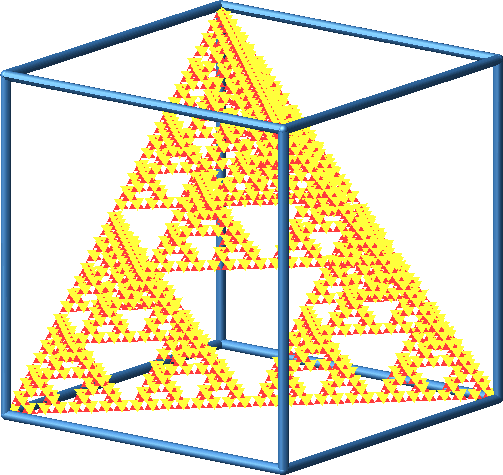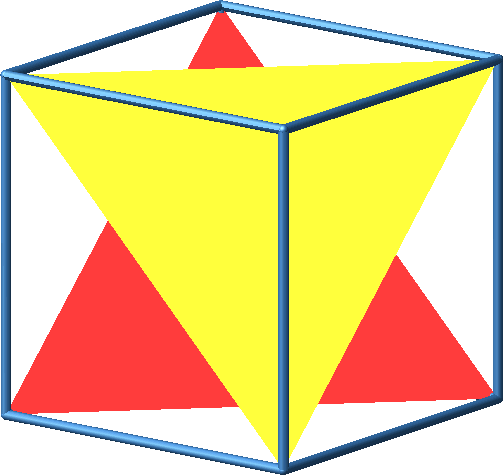
Abb. 9: Genesis des Sierpiński-Tetraeders

Abb. 10: Rotation des Sierpiński-Tetraeders

In den Frontalansichten auf eine Würfelseite erhalten wir ein Muster, welches den Rahmen vollständig ausfüllt (Abb. 11). In den Sichten auf eine Kante sehen wir ein affin verzerrtes Sierpiński-Dreieck oder gar nichts.

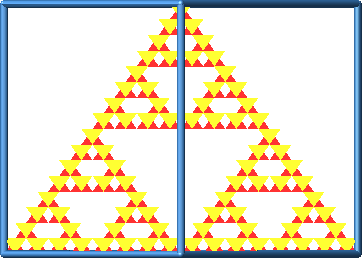
Abb. 11: Spezielle Ansichten

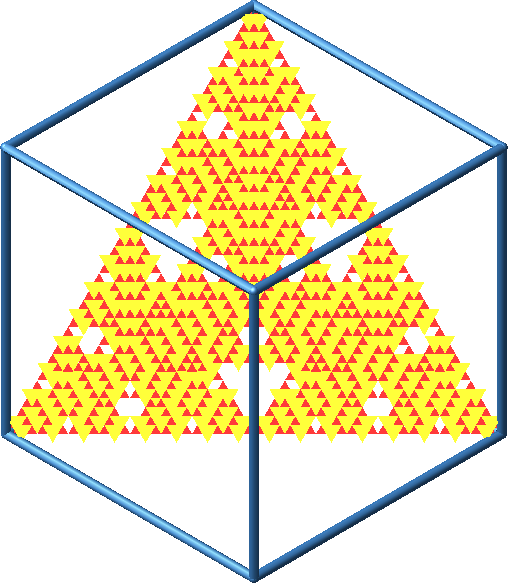
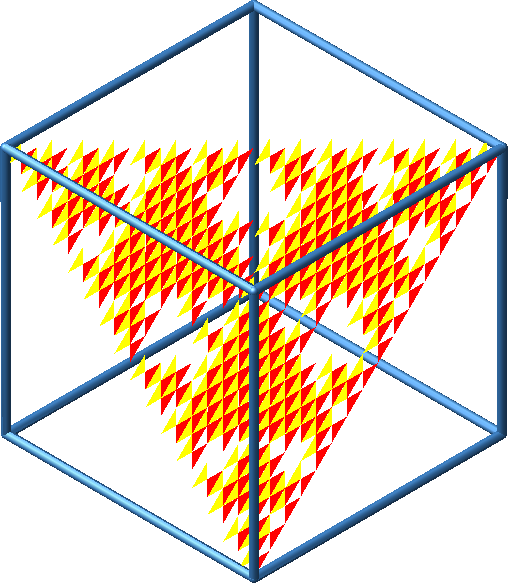
Abb. 12: Spezielle Ansichten

5 Punktspiegelung

Beim Konstruktionsprozess spiegeln wir jeweils einen der vier Teilwürfel an seinem Mittelpunkt, und zwar den Teilwürfel vorne-Mitte-oben (Abb. 13).

Abb. 13: Konstruktionsprozess mit Punktspiegelung

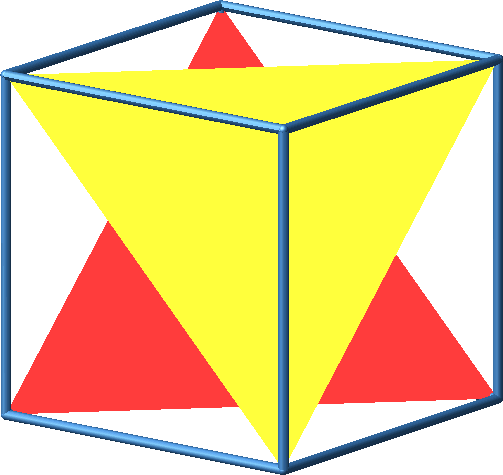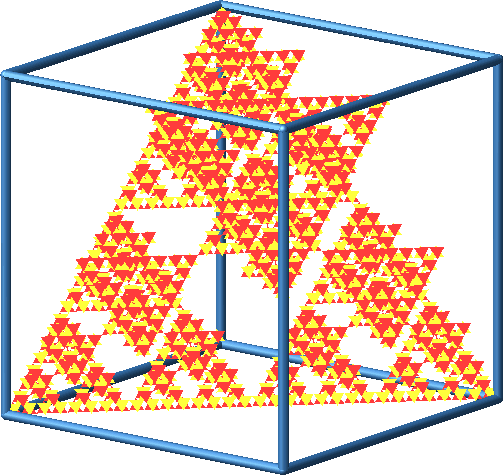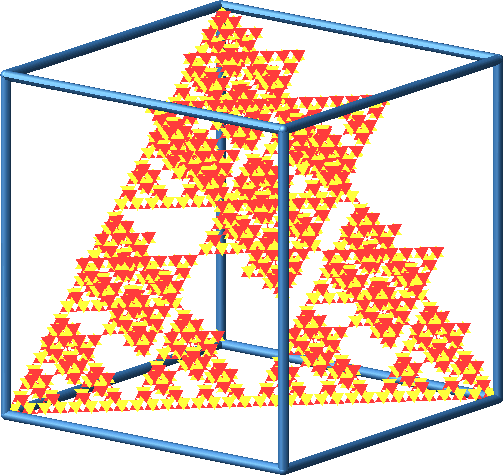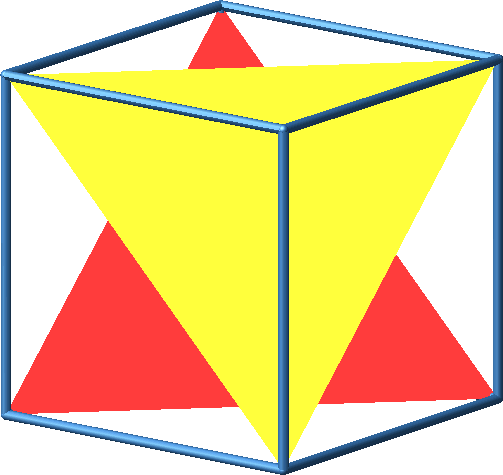
Abb. 14: Konstruktionsprozess mit Punktspiegelung

Abb. 15: Rotation

Die Muster in den speziellen Ansichten verändern sich (Abb. 16 und 17).

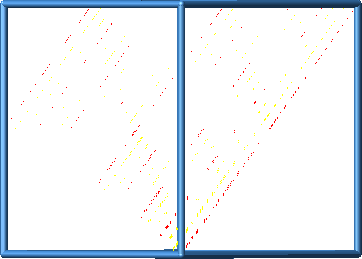
Abb. 16: Spezielle Ansichten

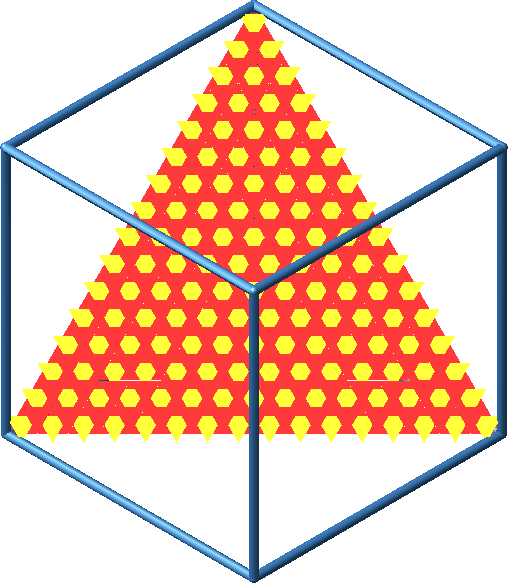
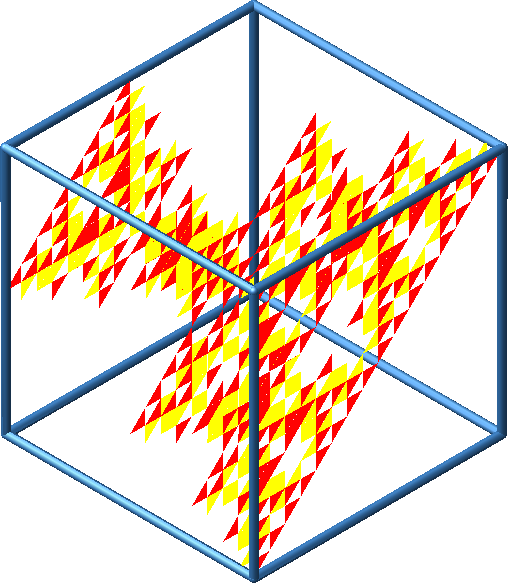
Abb. 17: Sicht über eine Ecke

6 Zwei Punktspiegelungen

Beim Konstruktionsprozess spiegeln wir jeweils zwei der vier Teilwürfel am Mittelpunkt, und zwar die beiden oberen Teilwürfel (Abb. 18).

Abb. 18: Konstruktionsprozess mit zwei Punktspiegelungen

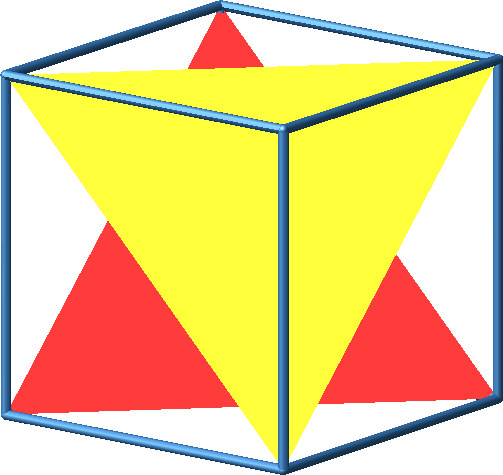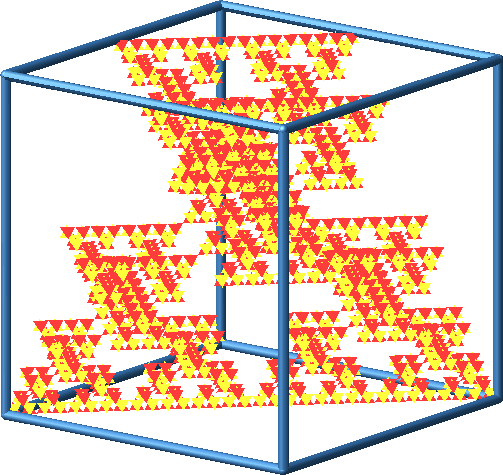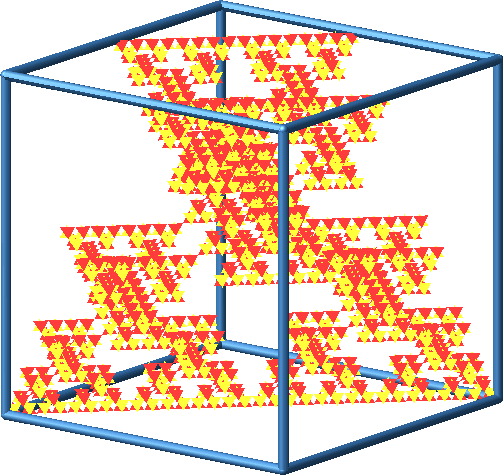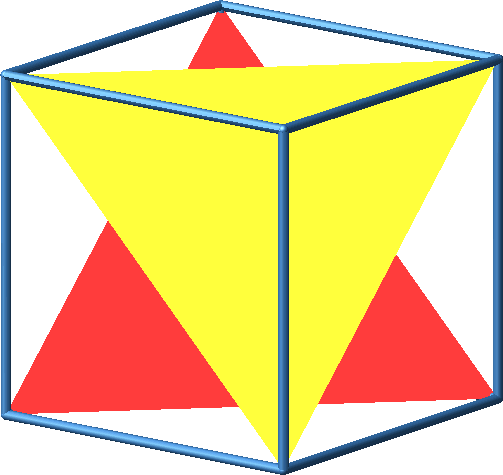
Abb. 19: Konstruktionsprozess mit zwei Punktspiegelungen

Abb. 20: Rotation

Abb. 21: Spezielle Sichten

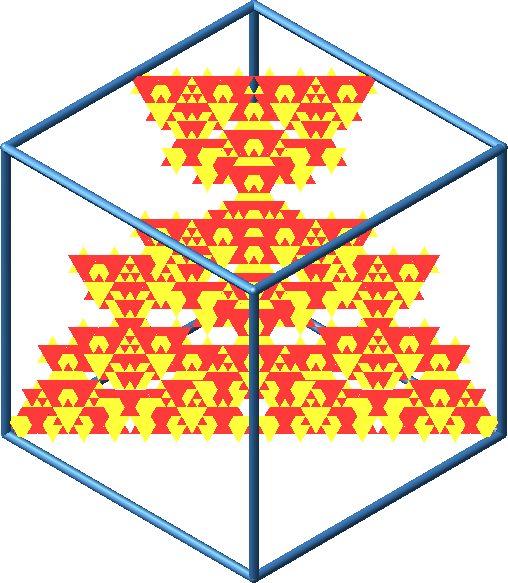
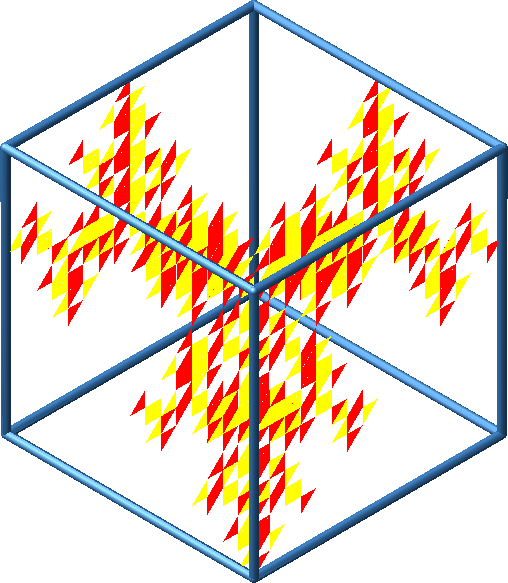
Abb. 22: Spezielle Sichten

Websites

Hans Walser: Würfelfraktal

http://www.walser-h-m.ch/hans/Miniaturen/W/Wuerfelfraktal3/Wuerfelfraktal3.html

Hans Walser: Würfelfraktal

http://www.walser-h-m.ch/hans/Miniaturen/W/Wuerfelfraktal2/Wuerfelfraktal2.html

Hans Walser: Schneeflocke

http://www.walser-h-m.ch/hans/Miniaturen/S/Schneeflocke/Schneeflocke.html

Hans Walser: Sierpinski, Cantor & Co.

http://www.walser-h-m.ch/hans/Miniaturen/S/Sierpinski/Sierpinski.htm

Hans Walser: Sierpinski-Dreieck

http://www.walser-h-m.ch/hans/Miniaturen/S/Sierpinski2/Sierpinski2.htm

Hans Walser: Sierpinski-Dreieck

http://www.walser-h-m.ch/hans/Miniaturen/S/Sierpinski3/Sierpinski3.htm

Hans Walser: Sierpinski-Fraktale

http://www.walser-h-m.ch/hans/Miniaturen/S/Sierpinski-Fraktale/Sierpinski-Fraktale.htm

Hans Walser: Sierpinksi-Tetraeder

http://www.walser-h-m.ch/hans/Miniaturen/S/Sierpinski-Tetraeder/Sierpinski-Tetraeder.html

Hans Walser: Sierpinksi-Tetraeder

http://www.walser-h-m.ch/hans/Miniaturen/S/Sierpinski-Tetraeder2/Sierpinski-Tetraeder2.html

Hans Walser: Sierpinski-Triangle

http://www.walser-h-m.ch/hans/Miniaturen/S/Sierpinski-Triangle/Sierpinksi-Triangle.mp4

Hans Walser: Sierpinski-Würfel

http://www.walser-h-m.ch/hans/Miniaturen/S/SierpinskiWuerfel/SierpinskiWuerfel.pdf