Hans Walser, [20230516]
Würfelgitter
Anregung: Name dem Autor bekannt
1 Problemstellung
In einem n×n×n-Würfelgitter sollen n2 Einheitswürfel so platziert werden, dass die Verbindungsgerade zweier Würfelmitten nirgends parallel zu einer Gitterrichtung ist.
2 Varianten zur Problemstellung
· In einem n×n×n-Würfelgitter sollen n2 Einheitswürfel so platziert werden, dass in jeder Gitterrichtung sämtliche Würfel gesehen werden. Es darf also kein Würfel einen anderen verdecken.
· In einem n×n×n-Schachbrett sollen n2 Türme so platziert werden, dass keiner den anderen schlagen kann.
3 Eine Lösung
Im Folgenden eine Lösung für n = 5 (Abb. 1). Diese Lösung funktioniert analog für beliebige n.
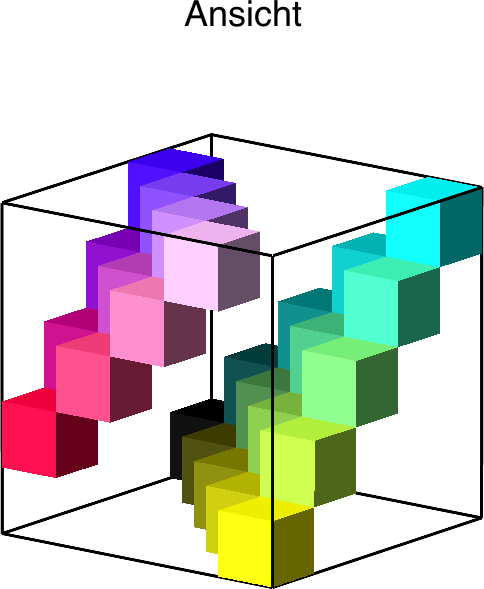
Abb. 1: Lösung
Die Farbgebung der Würfel orientiert sich am RGB-System. Die Gitterecke links unten ist der rote Pol, die Gitterecke rechts unten der grüne und die Gitterecke hinten oben der blaue. Die Gitterecke vorne oben ist der weiße Pol. Die Gitterecke hinten unten schwarz. Vorne unten haben wir gelb, links oben magenta und rechts oben cyan.
Die Abbildung 2 zeigt spezielle Sichten. Wir sehen in jeder Sicht die n2 Würfel quadratisch angeordnet.
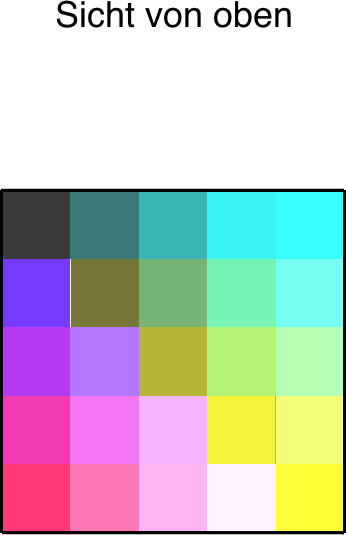


Abb. 2: Spezielle Sichten
4 Allgemein
Die Abbildung 3 zeigt die entsprechende Lösung für n = 1 bis 8.

Abb. 3: Allgemeine Lösung
Die Abbildung 4 zeigt die entsprechenden speziellen Sichten.



Abb. 4: Spezielle Sichten
5 Weitere Lösungen
Die Abbildung 5 zeigt eine weitere Lösung für n = 8.

Abb. 5: Weitere Lösung
Die Abbildung 6 zeigt die zugehörigen speziellen Sichten.
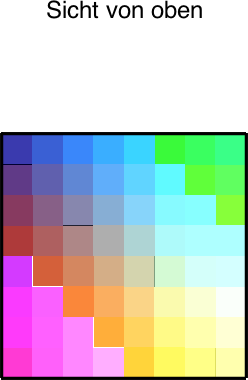
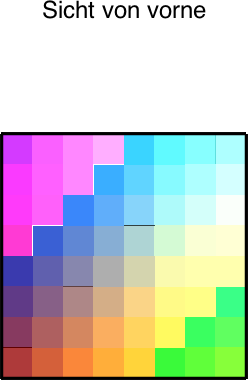

Abb. 6: Spezielle Sichten
In der Abbildung 7 werden die Schichten verschoben.

Abb. 7: Verschieben der Schichten
Die Abbildung 8 zeigt die entsprechenden speziellen Sichten.

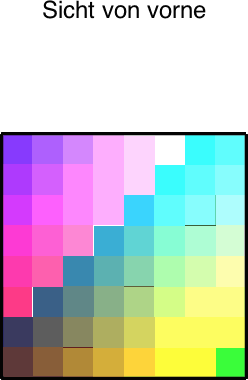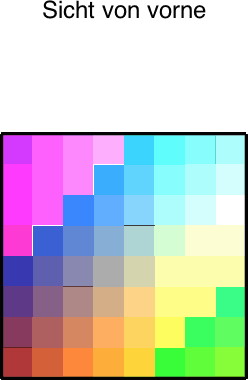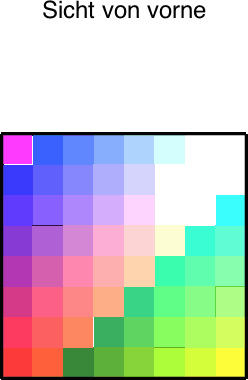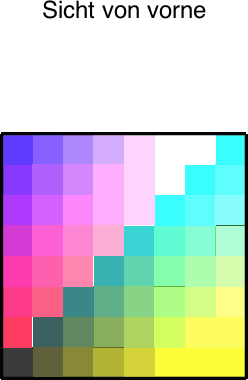

Abb. 8: Spezielle Sichten
Unsere Auflistung der Lösungen ist bei weitem nicht vollständig.
Weblinks
Hans Walser: Würfelfraktal
http://www.walser-h-m.ch/hans/Miniaturen/W/Wuerfelfraktal3/Wuerfelfraktal3.html