Hans Walser, [20231010]

Würfelhalbierung

Anregung: Swetlana Nordheimer, Berlin

1 Worum es geht

Raumvorstellung anhand des Würfels

2 Problemstellung

Ein Würfel (Abb. 1) soll in zwei kongruente Teilpolyeder zerlegt werden, deren Kanten ausschließlich auf Kanten, Seitenflächendiagonalen und/oder Raumdiagonalen des Würfels (Abb. 2) liegen.

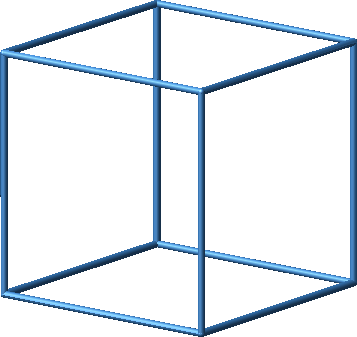
Abb. 1: Würfel

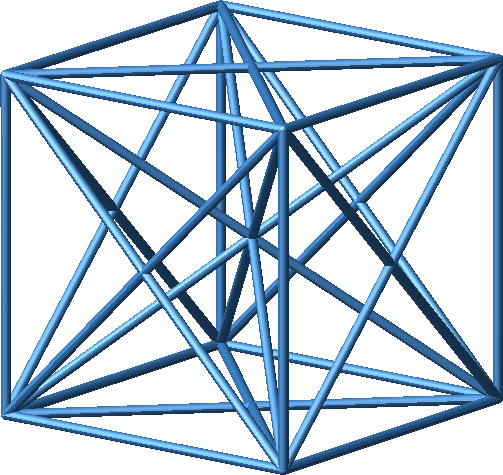
Abb. 2: Würfel mit Diagonalen

3 Beispiele

3.1 Beispiel 1

Das Beispiel 1 ist konvex.

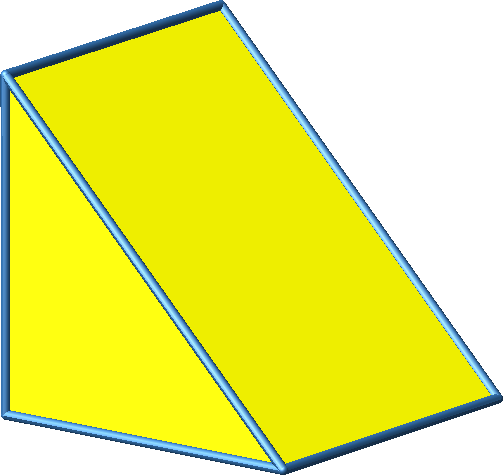
Abb. 3.1a: Beispiel 1

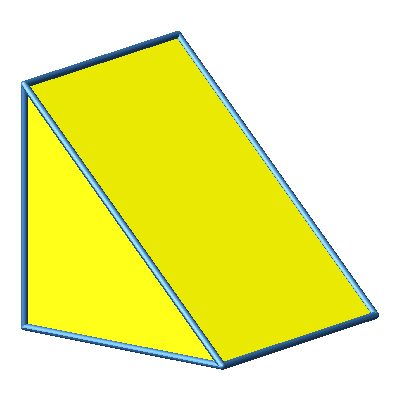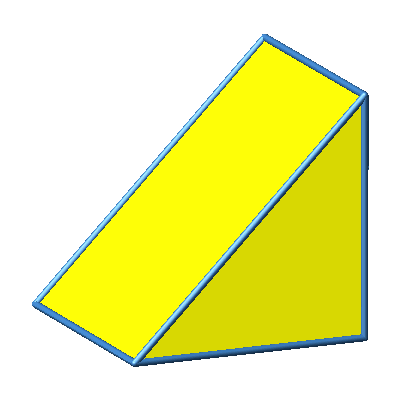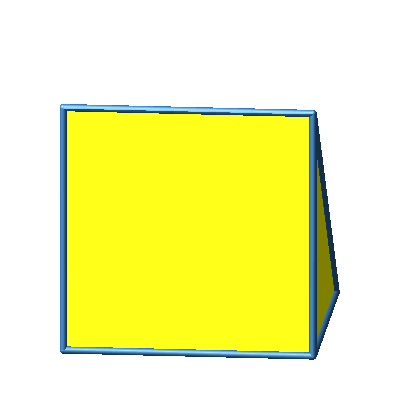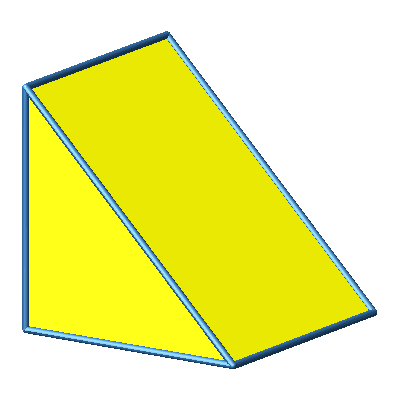
Abb. 3.1b: Beispiel 1

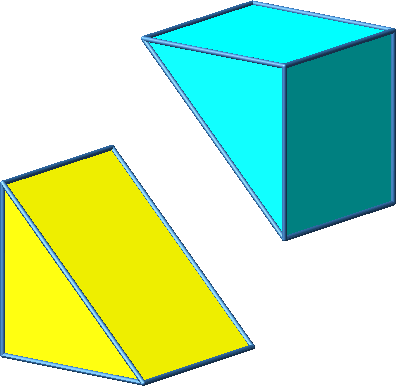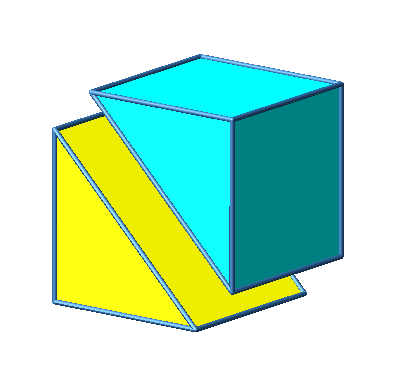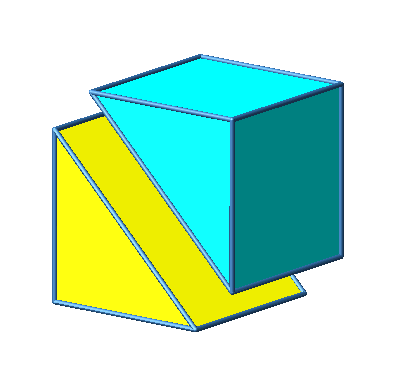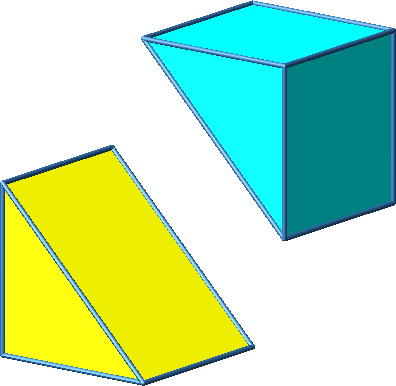
Abb. 3.1c: Beispiel 1

3.2 Beispiel 2

Das Beispiel 2 und alle folgenden Beispiele sind nicht konvex.

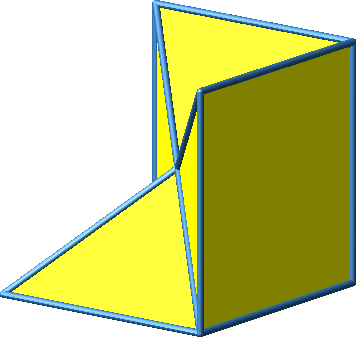
Abb. 3.2a: Beispiel 2

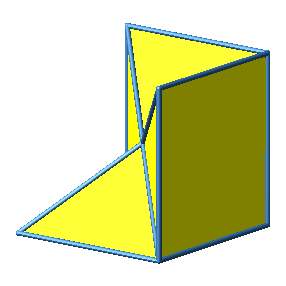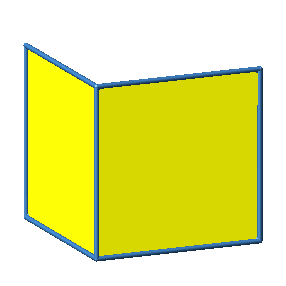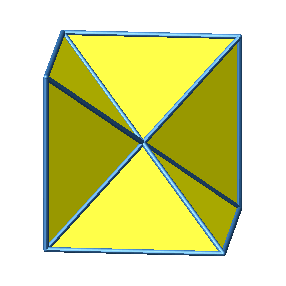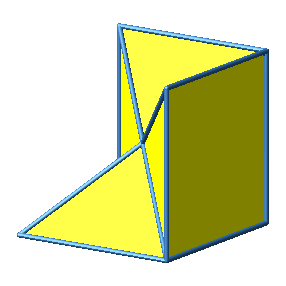
Abb. 3.2b: Beispiel 2

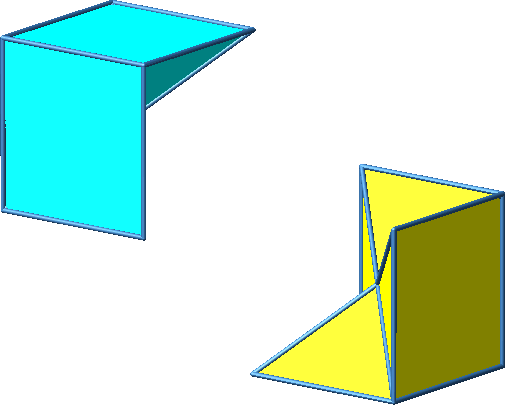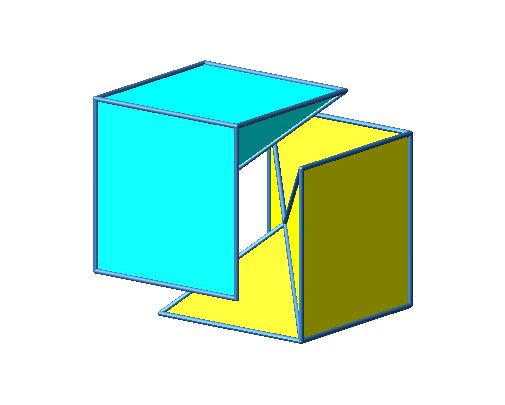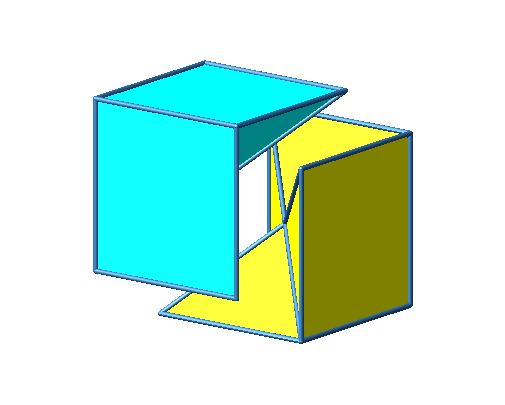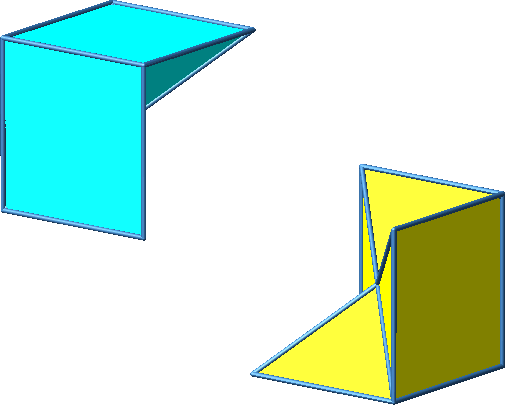
Abb. 3.2c: Beispiel 2

3.3 Beispiel 3

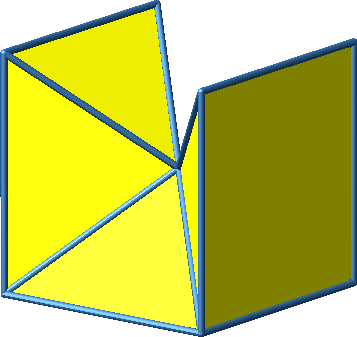
Abb. 3.3a: Beispiel 3

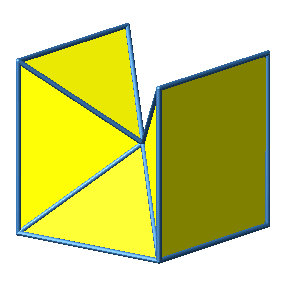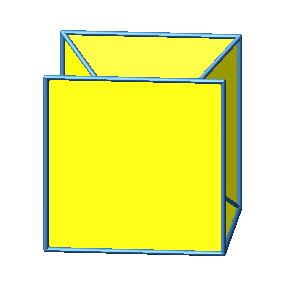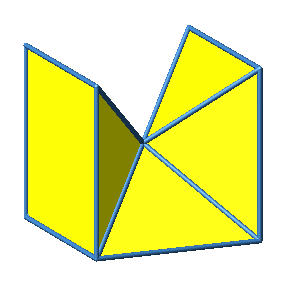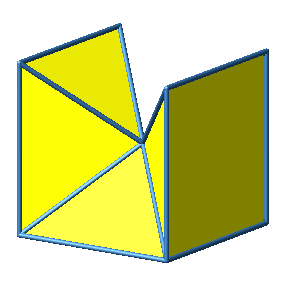
Abb. 3.3b: Beispiel 3

Abb. 3.3c: Beispiel 3

3.4 Beispiel 4

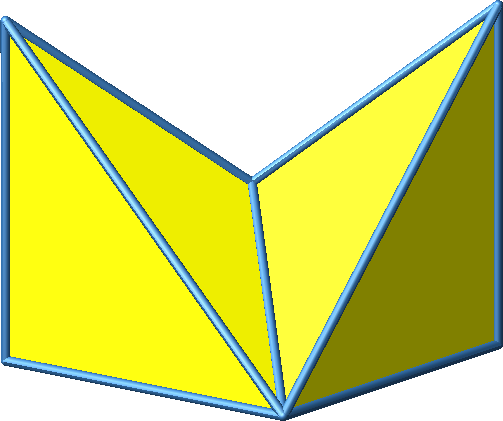
Abb. 3.4a: Beispiel 4

Abb. 3.4b: Beispiel 4

Abb. 3.4c: Beispiel 4

3.5 Beispiel 5

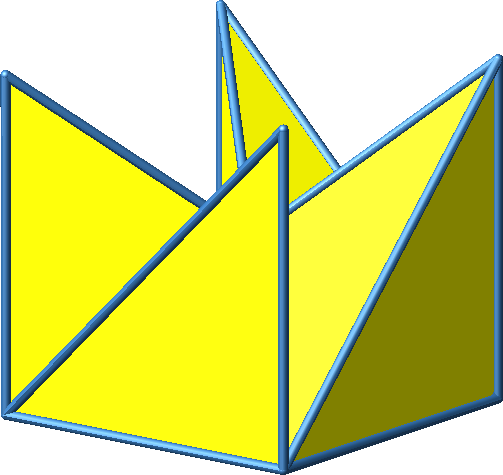
Abb. 3.5a: Beispiel 5

Abb. 3.5b: Beispiel 5

Abb. 3.5c: Beispiel 5

3.6 Beispiel 6

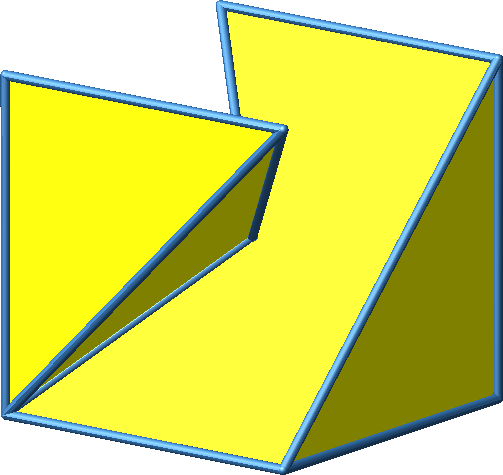
Abb. 3.6a: Beispiel 6

Abb. 3.6b: Beispiel 6

Die beiden Hälften können nicht zusammengeschoben werden (Abb. 3.6c). Es gibt Überschneidungen.

Abb. 3.6c: Beispiel 6

Auch das „Einschrauben“ führt zu Überschneidungen (Abb. 3.6d).

Abb. 3.6d: Beispiel 6

3.7 Beispiel 7

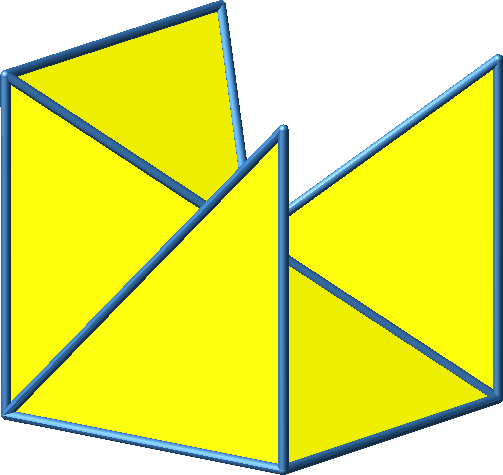
Abb. 3.7a: Beispiel 7

Abb. 3.7b: Beispiel 7

Abb. 3.7c: Beispiel 7. Zusammenfügen

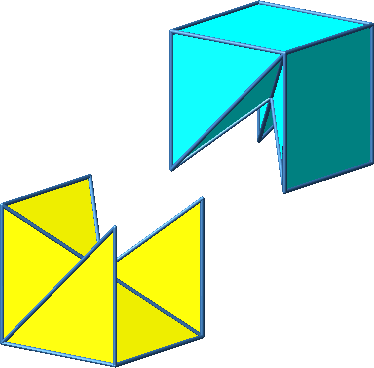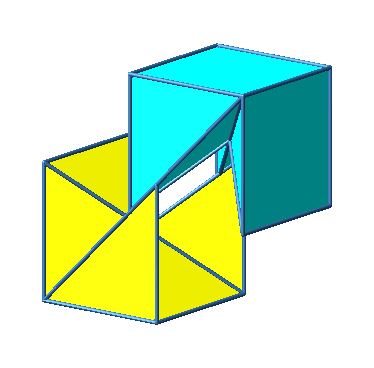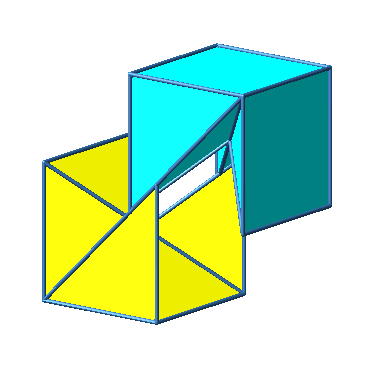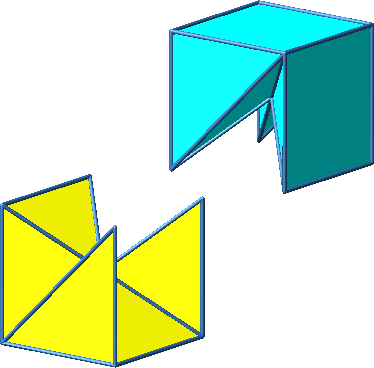
Abb. 3.7d: Beispiel 7. Zusammenfügen auf anderer Schiene

3.8 Beispiel 8

Abb. 3.8a: Beispiel 8

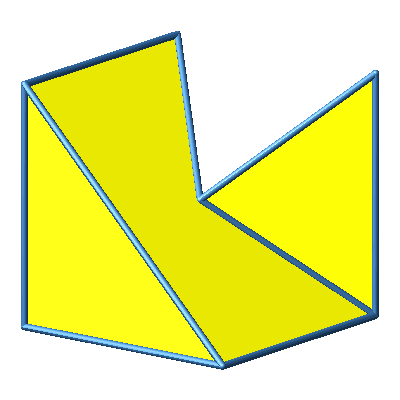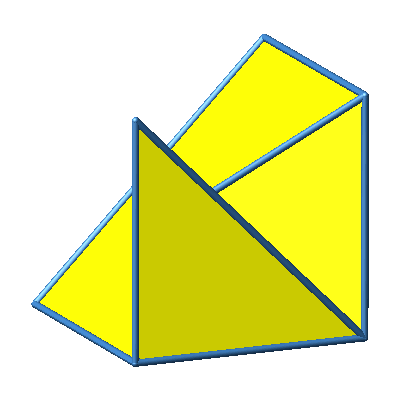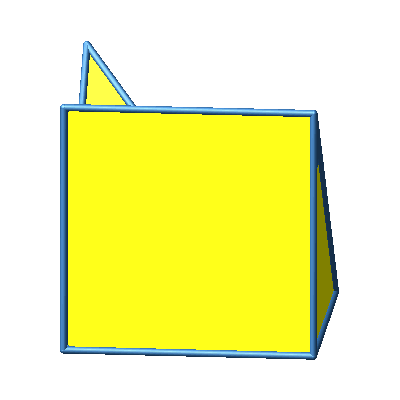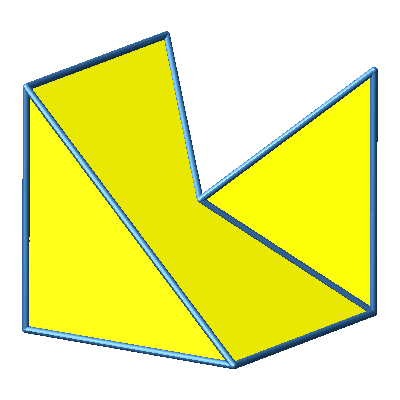
Abb. 3.8b: Beispiel 8

Abb. 3.8c: Beispiel 8. Zusammenfügen

Abb. 3.8d: Sicht von hinten

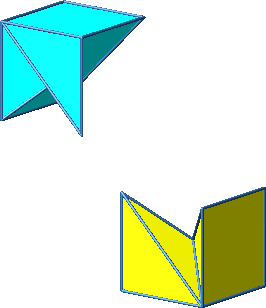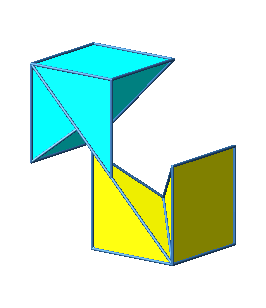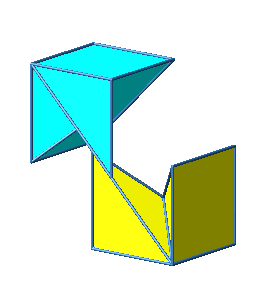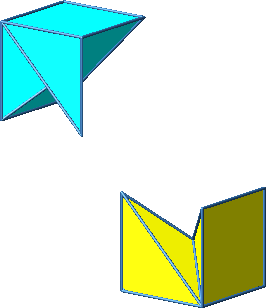
Abb. 3.8e: Andere Schiene

4 Ausblicke

Würfeldrittelung, Würfelviertelung, Würfelfünftelung (der Autor hat noch kein Beispiel für die Würfelfünftelung gefunden), Würfelsechstelung, Würfelzwölftelung

Weblinks

Hans Walser: Würfeldrittelung

https://walser-h-m.ch/hans/Miniaturen/W/Wuerfeldrittelung/Wuerfeldrittelung.html