Hans Walser, [20150108]

WŸrfelrezept

1     Worum geht es?

Gewusst wie ist besser als verstanden warum.

Es wird ein Rezept angegeben, einen WŸrfel schšn zu zeichnen.

Als Hilfsmittel verwenden wir eine gŠngige Grafik-Software.

2     Das Vorgehen

ZunŠchst zeichnen wir ein Quadrat, das der Boden des WŸrfels entsprechen soll, und eine Strecke, welche der Hšhe des WŸrfels entsprechen soll (Abb. 1).

 

Abb. 1: Bodenquadrat und Hšhe

 

Dann drehen wir das Bodenquadrat um einen beliebigen Winkel . Ich habe  gewŠhlt (Abb. 2). Die Software dreht im Uhrzeigersinn.

 

Abb. 2: Drehen

 

Nun stauchen wir das Bodenquadrat in der vertikalen Richtung um einen Faktor p. Ich habe p = 0.4 = 40% gewŠhlt (Abb. 3). Dadurch wird das Bodenquadrat ãrŠumlichÒ.

 

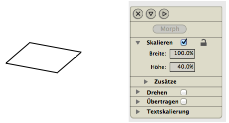
Abb. 3: Stauchen in der Hšhe

 

Nun kommt eine kleine Rechnung (Pythagoras lŠsst grŸ§en):

 

In unserem Fall hei§t das:

 

Jetzt stauchen wir die in der Abbildung 1 dargestellte Hšhe in der vertikalen Richtung mit dem Faktor q (Abb. 4).

 

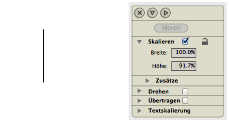
Abb. 4: Hšhe stauchen

 

Nun kšnnen wir vier Kopien dieser gestauchten Hšhe an den Ecken des gestauchten Bodenquadrates (das nun ein Parallelogramm ist) ansetzen (Abb. 5) und schlie§lich noch den Deckel aufsetzen.

 

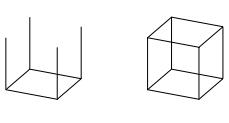
Abb. 5: Zusammenbau des WŸrfels

 

Damit ist der WŸrfel im Prinzip gezeichnet.

3     Kosmetik

Wir kšnnen nun noch einige Verschšnerungen anbringen.

Zum Beispiel kšnnen wir einen Raumeindruck generieren indem wir an den Kreuzungspunkten zweier WŸrfelkanten durch Unterbrechen ein ãVorne-HintenÒ suggerieren (Abb. 6). Dies geht auf zwei Arten: Aufsicht und Untersicht. †blicherweise wird die Aufsicht gewŠhlt.

 

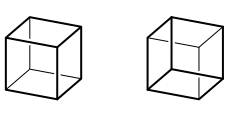
Abb. 6: Aufsicht und Untersicht

 

Wir kšnnen durch Kolorieren der SeitenflŠchen einen massiven WŸrfel vortŠuschen (Abb. 7).

 

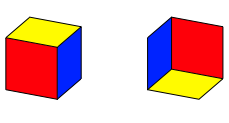
Abb. 7: Farbe kommt ins Spiel

 

Schlie§lich kšnnen wir drei paarweise orthogonale Einheitsvektoren zeichnen. Beide Bilder der Abbildung 8 stellen ein sogenanntes Rechtssystem dar.

 

Abb. 8: Einheitsvektoren

 

4     Hintergrund

Bei unserem WŸrfelbild handelt es sich um eine sogenannte Normalaxonometrie. Die beiden Winkel  und  werden als Eulersche Winkel bezeichnet. In unserem Beispiel ist:

 

Der Winkel  ist, wie wir schon gesehen haben, der Drehwinkel. Der Winkel  ist der Kippwinkel. Er gibt an, um wie viel der WŸrfel gegenŸber der Senkrechten nach vorn oder nach hinten gekippt ist. Wir kšnnen natŸrlich auch den Kippwinkel  frei wŠhlen und dann  und  berechnen.

Die Abbildung 9 zeigt Situationen mit verschiedenen Drehwinkeln bei konstantem Kippwinkel . Die Drehung erfolgt von oben gesehen im Uhrzeigersinn.

 

Abb. 9: Drehwinkel 0¡, 15¡, 30¡, 45¡, 60¡, 75¡, 90¡

 

Die Abbildung 10 zeigt Situationen mit verschiedenen Kippwinkeln bei konstantem Drehwinkel .

Abb. 10: Kippwinkel 0¡, 15¡, 30¡, 45¡, 60¡, 75¡, 90¡

 

Das wŠrÕs.